Copyright © 1996-1997 Angelo Veronesi

Esperimento 6: Proprietá dei gas

Back

1. Relazione tra pressione e temperatura

 

Apparecchiatura

  1. Ampolla collegata ad un vaso capillare piegato ad U tramite un tubo con rubinetto di chiusura
  2. Termometro digitale
  3. Vasca termica
  4. Acqua, mercurio
  5. Carta millimetrata

 

 

Teoria

  • La pressione e la temperatura di un gas sono legate dalla legge:

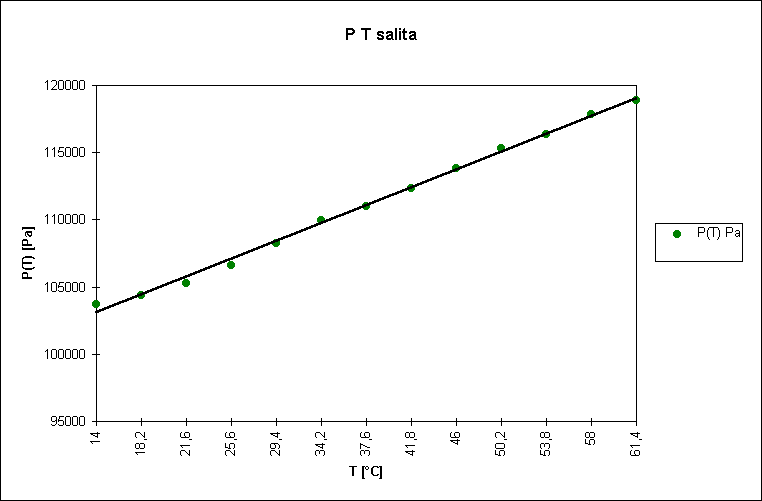
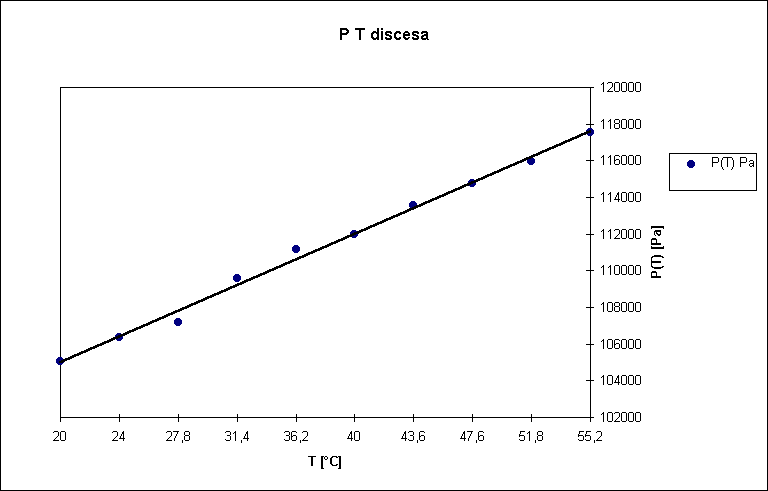
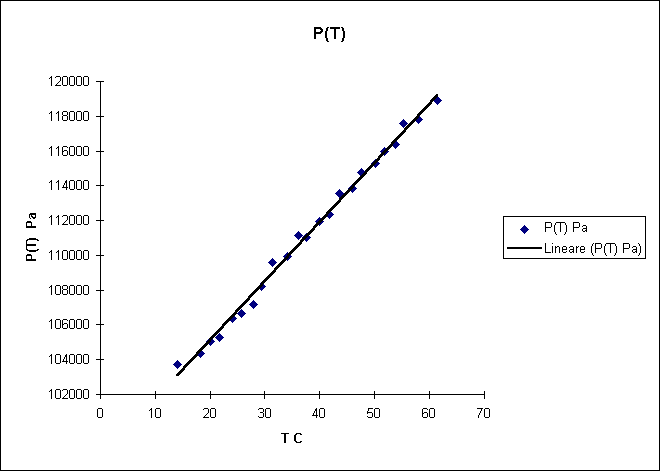
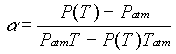    P(T) = P0 (1+a T)

    (P = pressione, T = temperatura)

    Se la condizione iniziale é tale che T = T0 si puó scrivere la relazione:

    P(T0) = P0 (1+a T0)

    Mettendo a sistema questa relazione con la precedente otteniamo:

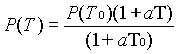
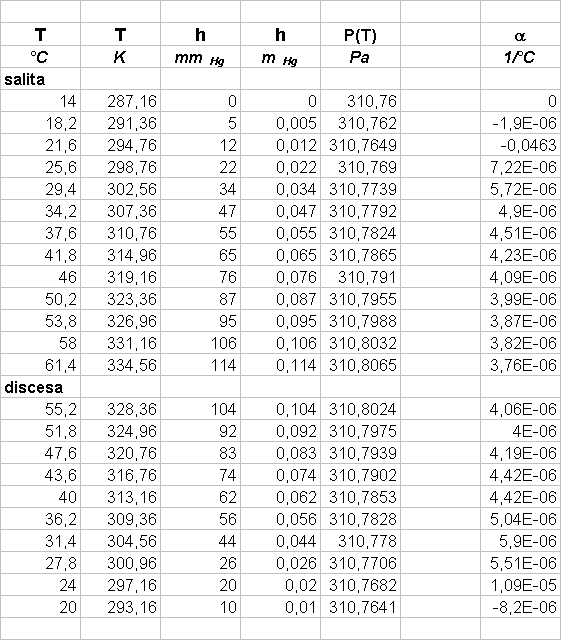
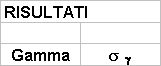
    Scopo di questo esperimento é calcolare a e stimarne l’errore.

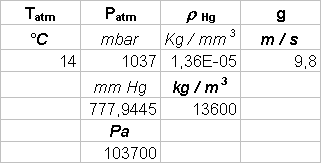
    Abbiamo aumentato la temperatura dell’aria contenuta nell’ampolla il cui volume poteva essere considerato costante, aumentando cosí proporzionalmente la pressione (in accordo con la legge di stato dei gas); in questo modo l’aria contenuta nell’ampolla comprimeva il mercurio contenuto nel capillare. Il mercurio nel capillare era sottoposto a due diverse pressioni: in un braccio del capillare era sottoposto alla pressione dell’aria dell’ampolla, nell’altro alla pressione atmosferica; dato che le due pressioni erano differenti il mercurio non era alla stesso livello nei due bracci e il D h tra i due livelli permetteva di calcolare la differenza fra la pressione atmosferica e la pressione dell’aria contenuta nell’ampolla. Se poniamo P(T0) = P atmosferica allora possiamo utilizzare la seguente relazione:

    r Hg D h g = P(T) - P(T0) = P(T) - Patm

    •

    Metodo

  • Dopo aver immerso l’ampolla nella vasca termica ed aver misurato la temperatura dell’acqua, abbiamo aperto il rubinetto del tubo di collegamento cosí che P(T0) = Patm ; successivamente abbiamo chiuso il rubinetto e abbiamo scaldato gradualmente l’acqua della vasca, rilevando 13 diverse temperature e i relativi D h del mercurio utilizzando la carta millimetrata. In seguito abbiamo ripetuto l’esperienza al contrario, lasciando raffreddare gradualmente l’acqua e rilevando 10 diverse temperature.
    •

    Dati sperimentali e analisi dei dati

  • Se calcolassimo a come media dei singoli a sperimentali relativi ad ogni temperatura otterremmo il seguente risultato:

    Calcoliamo invece a utilizzando il fit di una retta:

    y = ax + b

    P(T) = (a Patm) T + Patm

    Se non utilizzassimo la teoria degli errori otterremmo un valore di a totalmente errato; dall’esperimento otteniamo quindi 1/a = -289,293022 ° C , molto vicino al suo valore teorico (ricordiamo che 1/a = -273,16 ° C).

    Il risultato é influenzato soprattutto dagli errori nella lettura del D h di mercurio e dal fatto che, sebbene la temperatura dell’acqua nella vasca termica fosse praticamente uniforme, é impossibile affermare con assoluta certezza che la temperatura dell’aria all’interno dell’ampolla fosse uniforme, come si suppone durante l’esperimento.

    •

    2. Coefficiente adiabatico

     

    Apparecchiatura

    1. Bottiglia di Ruchardt
    2. Fotocellula
    3. Contatore collegato alla fotocellula
    4. Cronometro
    5. Pompa ad aria
    6. Palmer

     

    Teoria

  • Lo scopo di questo esperimento é calcolare il coefficiente adiabatico dell’aria (che é una miscela di gas, ma che approssima molto bene un gas biatomico); un metodo molto preciso e raffinato per determinare il coefficiente adiabatico g é il metodo di Ruchardt. La bottiglia di Ruchardt consiste di un tubo cilindrico di vetro, avente un diametro molto preciso, collegato ad una boccia di vetro di volume noto; nel cilindro di vetro viene inserito un cilindretto avente il diametro quasi uguale al diametro interno del cilindro di vetro (se i diametri fossero uguali il cilindretto non potrebbe scorrere nel cilindro di vetro e non si potrebbe eseguire l’esperimento). Il cilindretto puó cosí scorrere nel cilindro di vetro con un attrito minimo. Cadendo il cilindretto comprime l’aria e, se il cilindro di vetro é abbastanza lungo, puó superare il punto di equilibrio in cui il suo peso é bilanciato dalla pressione dell’aria; dopo aver superato il punto di equilibrio, il cilindretto é frenato dalla pressione ed é poi spinto verso l’alto. Il risultato é che il cilindretto oscilla intorno alla sua posizione di equilibrio ed ha un periodo molto rapido; purtroppo peró l’attrito, seppur ridotto al minimo, frena il cilindretto ed inoltre la posizione di equilibrio si muove verso il basso, perché ad ogni oscillazione c’é una perdita di aria, che passa nell’intercapedine tra il cilindro di vetro ed il cilindretto. Si possono osservare solo poche oscillazioni e per questo l’esperimento é stato modificato. Una pompa ad aria é stata collegata alla boccia di vetro ed é stato praticato un taglio all’altezza della posizione di equilibrio; la pompa immette aria nella boccia di vetro e spinge il cilindretto fino a quando supera il taglio praticato nel cilindro di vetro. In questo modo é possibile mantenere costante la posizone di equilibrio ed annullare l’azione degli attriti, permettendo cosí agli sperimentatori di studiare un congruo numero di oscillazioni. Dato che la pressione nella bottiglia alternativamente supera e scende sotto quella atmosferica, la temperatura dell’aria nella bottiglia alternativamente supera e scende sotto quella ambientale; ma le variazioni sono cosí rapide che non c’é alcun apprezzabile flusso di calore e quindi il sistema é essenzialmente adiabatico.

    Possiamo ricavare le seguenti relazioni:

    p V g = C = costante (p = pressione, V = volume)

    p = C V-g

    = -g C V-g -1

    = -g

    dp a = F (a = area di base interna cilindro di vetro)

    dV = a x (x = spostamento dalla posizione di equilibrio)

    •
  • m () = -g a2 x

    () = -g a2

    w = aÖ g ()

    T = Ö ()

    •
  • g = 4 ()2 ()4 ( R = raggio interno del cilindro di vetro)

    • Metodo

  • L’esperimento consiste nel misurare con massima precisione il periodo di oscillazione del cilindretto e calcolare cosí g ; per fare questo si posiziona la fotocellula lungo il cilindro di vetro in modo tale che ad ogni oscillazione il cilindretto la oscuri una sola volta e si azzera il contatore. Si fanno poi partire contemporaneamente il cilindretto e il cronometro e, dopo qualche centinaio di oscillazioni, si calcola il periodo del sistema dividendo il tempo trascorso per il numero di oscillazioni.
    •

    Dati sperimentali ed analisi dei dati

  • Otteniamo come risultato g = 1,405362 , molto vicino al suo valore teorico (g = 7/5 = 1,4).

    In questo esperimento le cause di errore dipendono esclusivamente dall’attrito fra il cilindretto mobile e il cilindro di vetro, che puó essere ulteriormente minimizzato lubrificando il cilindretto mobile con della comune grafite; é molto importante regolare bene il flusso d’aria della pompa in modo che la posizione di equilibrio si mantenga costante nel tempo.

    •