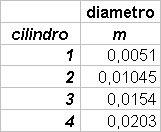
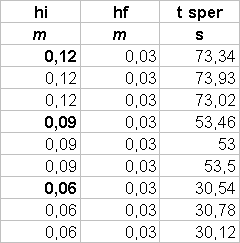
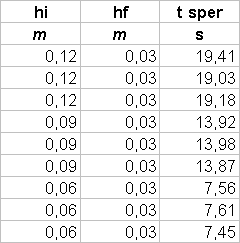
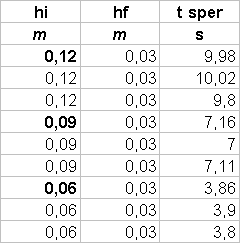
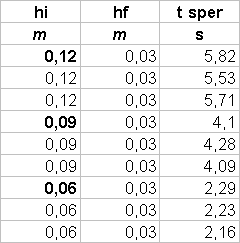
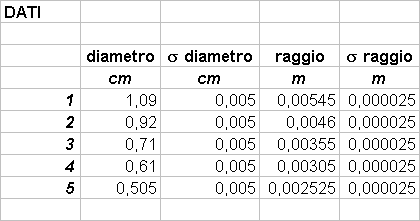
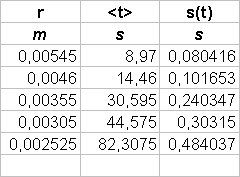
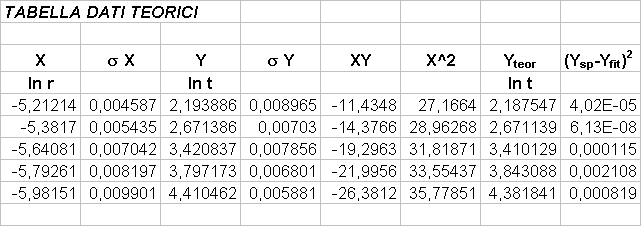
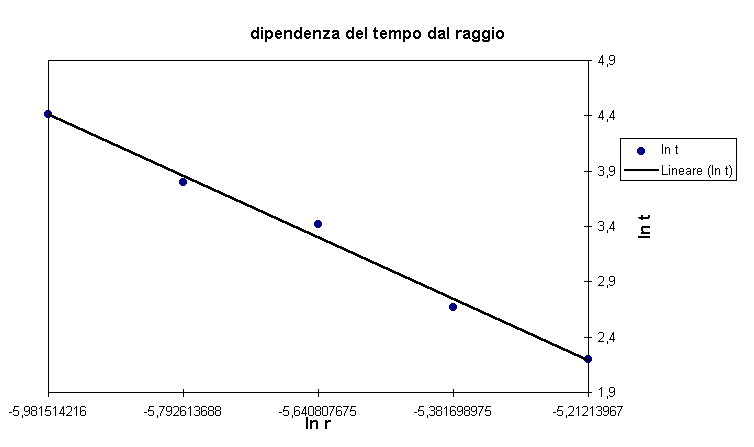
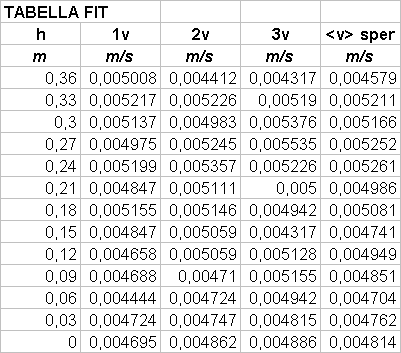
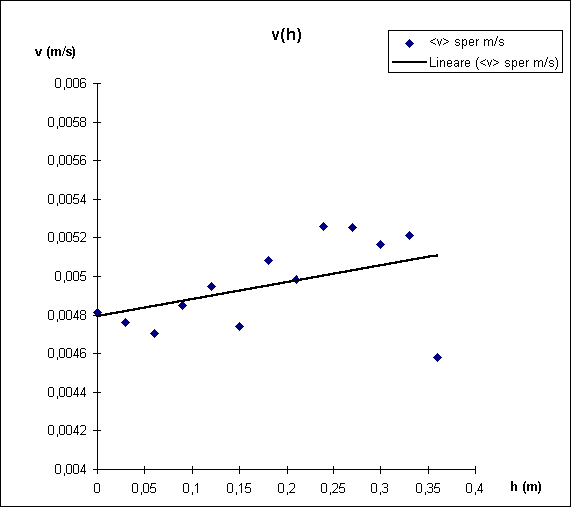
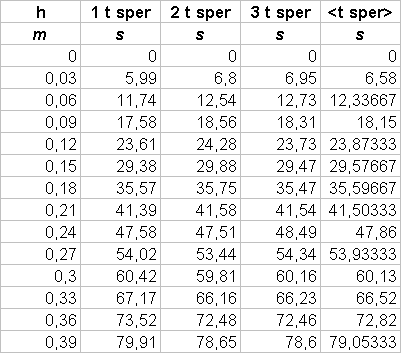
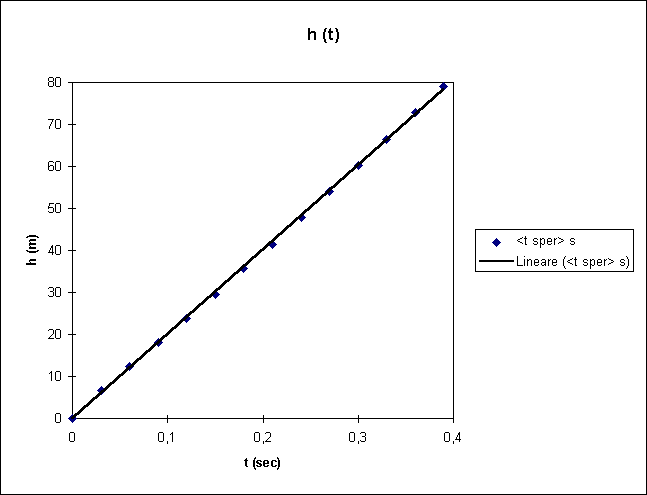
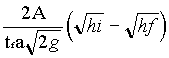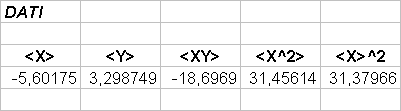Se infatti consideriamo un cilindro pieno d’acqua come un contenitore di un fluido ideale, vale il teorema di Bernoulli:

½rv² + rgh + Dp = cost

dove v é la velocità del fluido; h é l’altezza del cilindro, r é la densità del fluido e p é la pressione.

Possiamo applicare questo teorema alla situazione iniziale e finale del nostro sistema facendo attenzione affinché non si creino condizioni che non soddisfano quelle del teorema ( come per esempio la presenza di vortici d’acqua o l’attrito non trascurabile sulle pareti del cilindro).

P₀ + rgDh = P₀ + ½rv²

In questo modo possiamo calcolare la velocità di fuoriuscita del fluido ideale:

v =Infatti in cima al contenitore la velocità dell’acqua può essere considerata nulla, mentre all’altezza che si considera come origine del sistema (dato che non si può svuotare tutto il contenitore, altrimenti ci sarebbe troppo attrito tra le pareti del contenitore e il fluido) si può considerare solo la componente cinetica.La quantità infinitesima di acqua che esce in un certo intervallo di tempo si può scrivere come:dm = -r a v dt = r A dhdove a é la sezione del foro praticato sotto il recipiente ed A é la sezione del contenitore.In questo modo abbiamo specificato che la riduzione di massa dell’acqua in cima al cilindro é in relazione con quella che esce dal fondo. 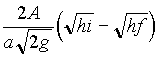Sostituendo e integrando nell’uguaglianza si ottiene che il tempo di uscita dell’acqua dal contenitore dipende da:t_f = se però analizziamo la situazione del sistema dell’acqua in termini newtoniani o anche in modo pratico, otteniamo un intervallo di tempo di svuotamento leggermente diverso a meno di una costante a.Infatti il peso della colonna d’acqua situata sopra il buco dipende da questa relazione:F= dp= m v^ = r a v^ ² dtquindi:= r a v^ ² v^ = si può notare che v ottenuta da Bernoulli é diversa da quella delle formule di Newton, questo perché bisogna considerare che la velocità di fuoriuscita ottenuta da Bernoulli é uno scalare, mentre quella ottenuta da Newton é un vettoriale, cioè ci dice il modulo e non la componente perpendicolare alla parete di fuoriuscita. Inoltre va sottolineato che il fenomeno di vena contracta influisce notevolmente sulla sezione del foro di uscita facendola diminuire.Considerando tutto questo possiamo riscrivere la relazione ottenuta per il tempo di fuoriuscita con un fattore di correzione a:t_f = 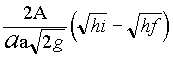Scopo dell’esperimento é quello di calcolare il coefficiente di vena contracta a per l’acqua.

Abbiamo misurato il diametro, e quindi il raggio delle sezioni del cilindro trovando che era identico per tutti:

R = 0,071 m

inoltre abbiamo misurato col calibro i fori praticati sotto i cilindri ed abbiamo trovato i seguenti valori:

In seguito abbiamo riempito ogni cilindro ad altezze diverse per più volte ottenendo una tabella sperimentale cosi fatta:

d = 0,0051m

2 cilindro

d = 0,01045

3 cilindro

d = 0,0154

4 cilindro

d = 0,0203

a =

quindi i risultati sono:

Abbiamo quindi verificato positivamente che il tempo di svuotamento corretto con a e quello sperimentale erano simili fra di loro, secondo la relazione già scritta.

Sappiamo inoltre che il risultato viene bene perché il nostro valore di a si avvicina molto alla Ö 2 che differenzia l’analisi di Bernoulli da quella di Newton:

v^ = (secondo Newton)

v = (secondo Bernoulli)

quindi la differenza tra le due velocità, e perciò il valore del coefficiente correttivo, deve essere all’incirca Ö 2.

Esperimento 5: Flusso granulare

La legge migliore da applicare al flusso di un fluido viscoso come la sabbia secondo noi é:

t = A r^-a

dove t é il tempo di svuotamento; r é il raggio del foro dell’imbuto.

Sembra rappresentare bene il tempo si svuotamento di un contenitore in funzione del raggio di fuoriuscita. Da notare il fatto che se r = 0, allora t = ¥ , cioè il caso di un contenitore senza il foro che non si svuoterà mai; inoltre dalla definizione delle costanti, il tempo di svuotamento viene sempre positivo.

Lo scopo di questo esperimento é determinare quanto é a nel caso di un fluido granulare, sapendo che per l’acqua a = 2.

e per i tempi di svuotamento:

Ipotizzando che sia vera le legge t = A r^-a , allora possiamo ottenere la relazione della miglior retta che passa per i punti che abbiamo trovato:

ln t = -a ln r + ln A

da dove si ottiene la seguente tabella teorica:

da cui si può ottenere:

ora, facendo il fit della retta

dove s² si ottiene attraverso la deviazione standard degli errori sul ln t e dove n sono i gradi di libertà del sistema.

da cui risulta un c²

con una P (c² > c²₀) = 49,36% che é un risultato molto buono.

D’altronde non si può non tener conto dell’apprezzabile risultato ottenuto per la misura di a.

Esperimento 5: Velocità del flusso granulare

Misurando il tempo impiegato dalla sabbia a scorrere da una tacca all’altra, abbiamo calcolato la velocità di percorrenza di tutti gli intervalli.

Per non commettere errori grossolani, abbiamo affidato il compito di rilasciare la sabbia e premere il cronometro ad una sola persona, mentre gli altri prendevano nota dei tempi controllando l’operato della prima.

Il primo metodo consiste nel determinare v(h), mentre il secondo determina la velocità come il coefficiente angolare di h(t).

da questi dati siamo giunti a determinare:

da cui siamo potuti risalire ai coefficienti della miglior retta:

e da qui siamo risaliti alla determinazione del c²:

quindi la P (c²> c²₀) =54,61%, per cui il risultato é molto buono.

così siamo riusciti a trovare i seguenti dati:

da cui i coefficienti della miglior retta:

Da notare, il fatto che la pendenza della retta esprime la velocità di scorrimento della sabbia, che perciò é una costante.

e da qui siamo risaliti alla determinazione del c²:

quindi la P (c²> c²₀) =65,10% , per cui il risultato é molto buono.

Inoltre un errore da tener conto é quello fatto per la determinazione di quando il livello superiore della sabbia sia passato da una tacca, infatti la superficie del fluido granulare non é piatta.

Comunque possiamo stabile che la velocità di scorrimento della sabbia é:

v = (0,00496± 9,7*10^-6) m/s.