La specificità dell’esperimento non comporta assolutamente l’utilizzo di aggeggi strani o complicati, infatti abbiamo utilizzato strumenti non difficili da reperire come due bottiglie di vetro e un normale sistema per generare frequenze.

L’esperimento si basa essenzialmente sulla constatazione che soffiando attraverso il collo di una bottiglia viene emessa una certa nota. L’aria contenuta nel collo della bottiglia, infatti viene spinta verso il gas contenuto all’interno, che si comprime e si dilata come se fosse un oscillatore armonico.

Il gas si comporta come una molla che può vibrare solo ad una certa frequenza n, infatti se noi poniamo:

F = pr² Dp

dove F é la forza applicata alla massa del gas che si comporta come una molla; r é il raggio del collo della bottiglia e Dp é l’aumento della pressione all’interno della bottiglia.

Dp =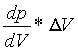

da cui si può arrivare alla determinazione della comprimibilitá :

k =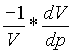

Tutto questo succede semplicemente per il fatto che la massa di gas del collo della bottiglia comprime di una certa quantità il volume del gas contenuto nella bottiglia.

m = r pr² l

dove m è la massa del gas che si trova nel collo della bottiglia, r è la densità del gas ed " l " l’altezza del collo. Poniamo dunque l’ipotesi che la massa del gas si muova come se fosse un corpo solido appoggiato sopra una molla. Possiamo ipotizzare ciò perché la massa che viene spostata è molto più piccola di quella del gas che funge da molla.

DV = pr² x

dove DV è la variazione del volume, quindi è la misura della compressione del gas che funge da molla ed x invece è lo spostamento teorico della massa di gas del collo della bottiglia.

Quindi sapendo che la forza applicata alla massa del gas all’interno della bottiglia si comporta come una molla:

F = pr² Dp = m (d²x/dt²)

In questo modo risulta chiaro che il sistema si comporta come se fosse un oscillatore armonico:

(d²x/dt²) = - ( pr² / r K V l ) * x

Notando poi che la velocità del suono in un gas è:

c = 1/ Ö (r K)

Possiamo scrivere che l’unica frequenza che può far risuonare, quindi oscillare questo oscillatore è data dalla relazione:

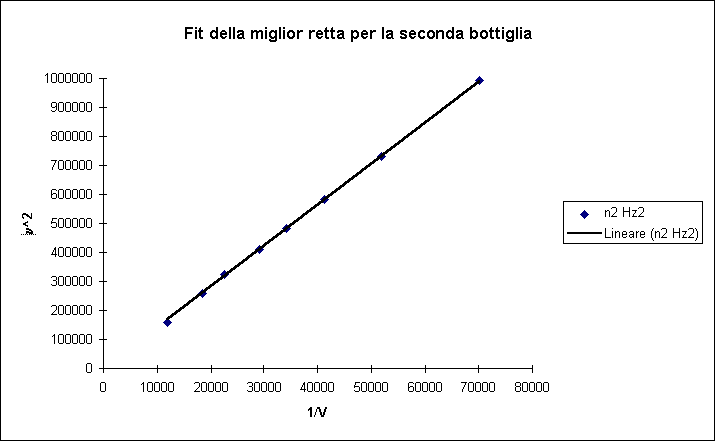
n = w /2 p = (1/ 2p) * Ö ( pr² c² / l V )

Sa questa formula possiamo poi notare che la frequenza prodotta dall’oscillazione è diversa a seconda del volume della bottiglia e della lunghezza del collo della bottiglia, oltre che dalla sezione del collo.

Con questa semplice relazione è quindi possibile risalire ad una buona approssimazione della velocità del suono nell’aria.

Per misurare il volume delle bottiglie abbiamo semplicemente riempito d’acqua le bottiglie fino alla base del collo e poi misurato per quattro volte il volume dell’acqua richiesta attraverso cilindri graduati e pipette.

Le bottiglie sono state riempite gradualmente con quantità definite di acqua attraverso la pipetta, cosi’ da conoscere in ogni momento il volume delle bottiglie. Ovviamente ogni tanto controllavamo nei cilindri graduati che l’acqua che avevamo nella bottiglia fosse proprio quella che ci aspettavamo.

Ogni volta che riempivamo la bottiglia, ed il suo volume diminuiva, cercavamo la frequenza che faceva risuonare la bottiglia grazie al frequenzimetro, ed ogni volta annotavamo la frequenza che faceva oscillare il gas contenuto all’interno della bottiglia con conseguente emissione del suono.

all’altezza del collo deve essere però aggiunta una quantità correttiva che fa funzionare bene il modello, anche se abbiamo misurato tutto come se il gas contenuto nel collo della bottiglia si muovesse come se fosse un solido verso l’interno della bottiglia.

l oggettiva = l + 0,8 d

quindi:

Abbiamo inoltre controllato che i nostri risultati corrispondessero al vero misurando anche il volume del collo della bottiglia:

dove il volume del collo sperimentale e’ quello che abbiamo trovato attraverso la misurazione del volume del collo della bottiglia, mentre il volume del collo teorico è quello trovato applicando le regole geometriche per la determinazione del volume dei solidi.

Da questi risultati siamo risaliti alla miglior retta che passa per quei punti:

Abbiamo posto y = n² e x = 1/V, li abbiamo inseriti nella seguente relazione trovata:

n² = ( r² c² / 4p l _ogg. ) 1/V

ed in questo modo abbiamo trovato i due grafici ed i due valori della velocità del suono nell’aria per ogni bottiglia.

In questo modo siamo potuti risalire al valore di c, dato dalla pendenza della miglior retta:

c = Ö ( (16p l _ogg. a) / d²)

dove a è la pendenza della miglior retta.

la seconda bottiglia, invece ha un valore di c = ( 343,884 ± 0,0004 ) m/s

Concludendo e facendo la media pesata delle due velocità del suono ottenute, si ha:

c = ( 349,182 ± 0,0003 ) m/s