Qualsiasi corpo rigido può essere
utilizzato come pendolo; infatti per ogni corpo esteso
che oscilli attorno ad un asse orizzontale vale la
seguente legge :I a = -mgd sinq
dove I é il momento di inerzia del
corpo rispetto all’asse attorno a cui oscilla, a é
l’accelerazione angolare, m é la massa del corpo e
d é la distanza fra il centro di massa del corpo e
l’asse di rotazione. Da questa legge ricaviamo che:
w 2
= 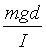 T = 2p Ö (
T = 2p Ö (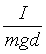 )
)
Sostituendo nella seconda relazione la
corretta espressione di I ottengo:
d2 - T2gd/4p 2
+ G2 = 0
dove G é il raggio di girazione.
Questa é una equazione di secondo
grado in d, quindi:
(d1+d2) = 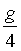 (
(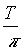 )2 ® g = 4(d1+d2)(
)2 ® g = 4(d1+d2)(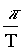 )2
)2
Questa relazione afferma che per ogni
corpo esistono due punti distinti attorno ai quali si
misura lo stesso periodo di oscillazione; il pendolo di
Kater é costruito in modo da poter oscillare attorno a
due coltelli posti alle sue estremità e ha un peso
mobile che può essere fissato in un punto qualsiasi tra
i due coltelli. In questo modo é possibile variare la
distanza dei due centri di rotazione dal centro di massa
del pendolo senza variare pero la loro somma, che é pari
alla distanza fra i due coltelli. Lo scopo
dell’esperimento é fissare il peso mobile in modo
tale che i periodi di oscillazione rispetto a ciascun
coltello siano pressoché identici; dopo aver determinato
questo "periodo comune " é possibile calcolare
l’accelerazione di gravità locale utilizzando la
formula:
g = 4 (d1+d2) (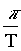 )2
)2
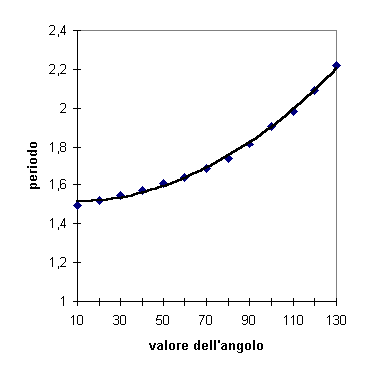
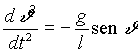 la legge viene
approssimata dicendo che il periodo è
la legge viene
approssimata dicendo che il periodo è 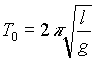 , questa formula
risulta praticamente esatta per J ® 0. Quando
l’angolo diventa grande e il sen(J ) non è
più paragonabile a J possiamo approssimare il periodo con la
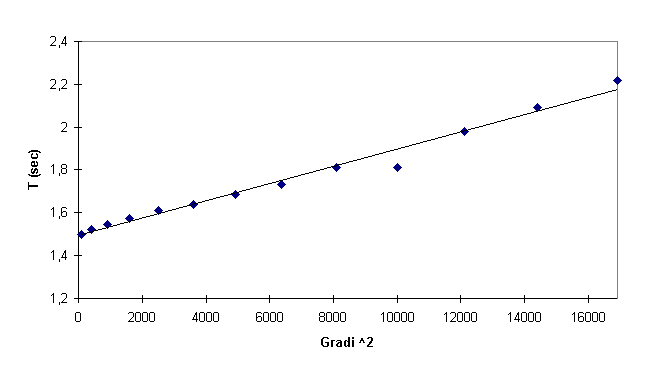
seguente formula, ottenuta dallo sviluppo di Taylor [ T(J ) = T0
+ a J 2 + b J 4...]
, questa formula
risulta praticamente esatta per J ® 0. Quando
l’angolo diventa grande e il sen(J ) non è
più paragonabile a J possiamo approssimare il periodo con la
seguente formula, ottenuta dallo sviluppo di Taylor [ T(J ) = T0
+ a J 2 + b J 4...]