m1= massa peso
m2= massa carrello
h= 0.30 m
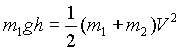
ovvero
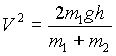
Esperimento 2 : Rotaia a cuscino d’aria
Apparecchiatura:
Teoria:
Nel nostro esperimento abbiamo testato:
1) Verifica della legge D U=D K
m1= massa peso
m2= massa carrello
h= 0.30 m
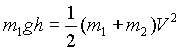
ovvero
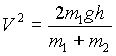
Dati sperimentali
0,027118 |
0,309131 |
0,3 |
0,13 |
0,14 |
|||
0,14 |
|||
0,14 |
|||
0,14 |
|||
0,14 |
|||
0,13 |
|||
0,14 |
0,027118 |
0,209131 |
0,85 |
0,03 |
0,027118 |
0,309131 |
0,73 |
0,02 |
0,027118 |
0,409131 |
0,64 |
0,02 |
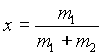
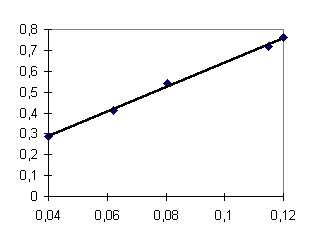
0,114785 |
0,72 |
0,05 |
0,080648 |
0,54 |
0,03 |
0,062161 |
0,41 |
0,02 |
5,93 |
0,92 |
0,049 |
0,004 |
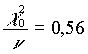 e
e ![]()
Il risultato é buono, tenendo conto che l’attrito sulla rotaia non é del tutto assente e che non sempre il peso cadeva esattamente per 30 cm.
2) Conservazione quantitą di moto
Per calcolare p1 e p2 abbiamo posizionato il carrello2 tra le due fotocellule e poi abbiamo spinto il carrello1 contro il carrello2; in questo modo abbiamo misurato molte V1 e V2 per ogni coppia di masse m1 e m2 e abbiamo potuto calcolare p1 e p2 con i relativi errori.
Dati sperimentali
0,199801 |
0,211041 |
0,18 |
0,02 |
0,16 |
0,01 |
0,211041 |
0,199801 |
0,11 |
0,01 |
0,09 |
0,01 |
0,199801 |
0,311041 |
0,13 |
0,04 |
0,15 |
0,04 |
0,311041 |
0,199801 |
0,12 |
0,02 |
0,08 |
0,01 |
0,299801 |
0,311041 |
0,19 |
0,05 |
0,17 |
0,04 |
0,311041 |
0,299801 |
0,21 |
0,04 |
0,15 |
0,02 |
0,199801 |
0,411041 |
0,19 |
0,03 |
0,22 |
0,01 |
0,411041 |
0,199801 |
0,19 |
0,02 |
0,11 |
0,01 |
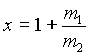 e
e 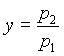
0,114785 |
0,72 |
0,05 |
0,080648 |
0,54 |
0,03 |
0,062161 |
0,41 |
0,02 |
![]()
Poniamo ![]() e otteniamo
e otteniamo
-0,98 |
0,18 |
0,53 |
0,13 |
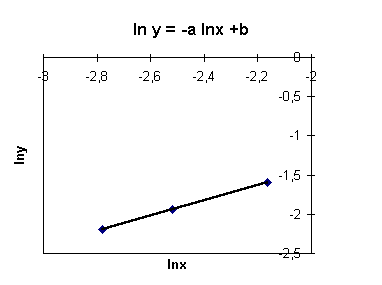
Il test del c 2 dą il seguente risultato:
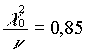 e
e ![]()
Il risultato é soddisfacente
Dati sperimentali
0,2 |
0,43 |
0,5 |
0,2325 |
0,005 |
0,25 |
0,52 |
0,4 |
0,1923 |
0,004 |
0,29 |
0,6 |
0,3448 |
0,1666 |
0,003 |
0,31 |
0,65 |
0,3225 |
0,1538 |
0,002 |
0,33 |
0,68 |
0,303 |
0,147 |
0,002 |
0,37 |
0,76 |
0,2702 |
0,1315 |
0,002 |
0,4 |
0,82 |
0,25 |
0,1219 |
0,001 |
0,453 |
0,01 |
0,008 |
0,004 |
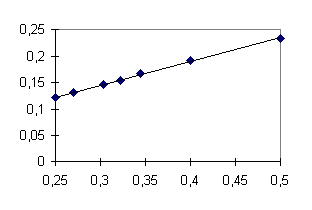
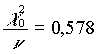 e
e ![]()
3) Accelerazione di gravitą
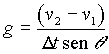
v1= vel.passaggio prima fotocellula
v2= vel.passaggio seconda fotocellula
D t = tempo per andare da una fotocellula all’altra
Dati sperimentali
h= 2,5 ± 0,01 cm
sin q = h/l = 0,0125
Abbiamo ottenuto i seguenti dati sperimentali
0,27 |
0,15 |
1,93 |
0,3703 |
0,6666 |
12,2818 |
1,28 |
0,26 |
0,15 |
1,91 |
0,3846 |
0,6666 |
11,8115 |
1,22 |
0,26 |
0,15 |
1,91 |
0,3846 |
0,6666 |
11,8366 |
1,18 |
0,39 |
0,16 |
2,35 |
0,2564 |
0,625 |
12,548 |
1,23 |
0,26 |
0,15 |
1,92 |
0,3846 |
0,6666 |
11,75 |
1,12 |
0,42 |
0,17 |
2,45 |
0,238 |
0,5882 |
11,4351 |
1,34 |
0,35 |
0,16 |
2,22 |
0,2857 |
0,625 |
12,227 |
1,16 |
0,32 |
0,16 |
2,14 |
0,3125 |
0,625 |
11,6822 |
1,25 |
0,29 |
0,15 |
2,03 |
0,3448 |
0,6666 |
12,6817 |
1,13 |
0,21 |
0,14 |
1,65 |
0,4761 |
0,7142 |
11,5442 |
1,04 |
0,39 |
0,16 |
2,37 |
0,2564 |
0,625 |
12,4421 |
1,36 |
0,21 |
0,16 |
1,03 |
0,4761 |
0,625 |
11,565 |
1,25 |
0,28 |
0,18 |
1,27 |
0,3571 |
0,5555 |
12,4976 |
1,2 |
0,21 |
0,16 |
1,02 |
0,4761 |
0,625 |
11,6784 |
1,27 |
11,99 |
1,21 |