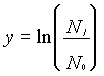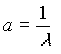Definiamo la formula: ![]() in cui Nr sono le
biglie che non hanno ancora urtato alla distanza r,
mentre K*Nr*dr sono le biglie che urtano nello
spazio dr.
in cui Nr sono le
biglie che non hanno ancora urtato alla distanza r,
mentre K*Nr*dr sono le biglie che urtano nello
spazio dr.
A questo punto possiamo ottenere una formula che lega le biglie che non hanno ancora urtato alla distanza r:
![]()
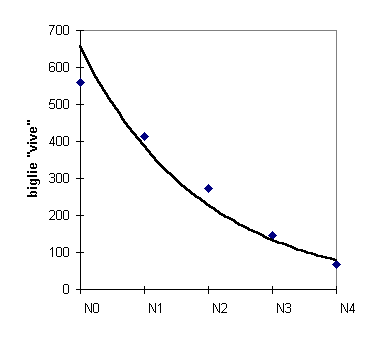
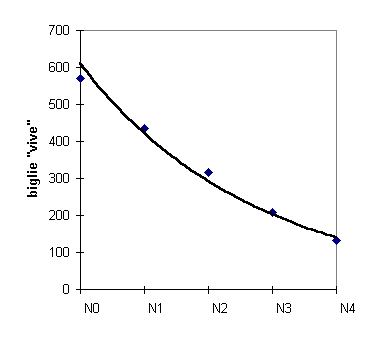
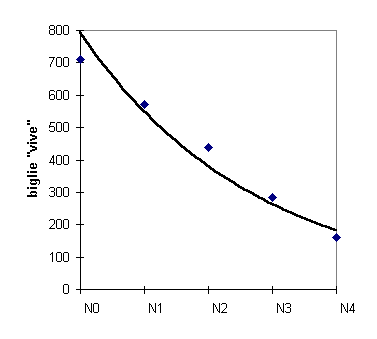
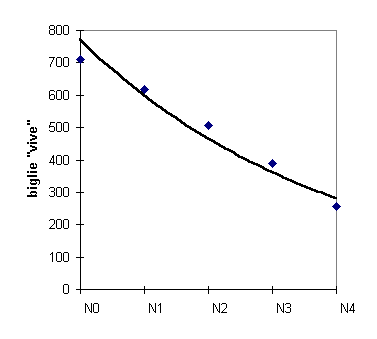
nella formula compare la costante l chiamata proprio libero cammino medio che determina la formula della curva il cui grafico mostra il numero di biglie (molecole) che non hanno ancora urtato.
Possiamo definire la formula ![]() che ci indica
l’area coperta dalle biglia nel tempo t.
che ci indica
l’area coperta dalle biglia nel tempo t.
Indicando con h il numero di
ostacoli per unitą di superficie si vede che in un tempo
t si hanno h ![]() collisioni.
collisioni.
Definendo il tempo che intercorre fra
gli urti come: 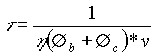 possiamo definire l come:
possiamo definire l come:
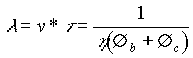
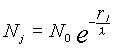
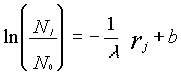 (in cui)
(in cui)