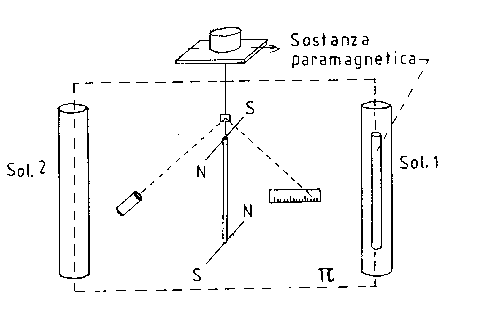
7. MISURA DELL’INTENSITA’ DI MAGNETIZZAZIONE DI UNA SOSTANZA
Scopo dell’esperienza
Ci proponiamo di determinare attraverso il magnetometro astatico
Descrizione dell’esperienza ed apparato sperimentale

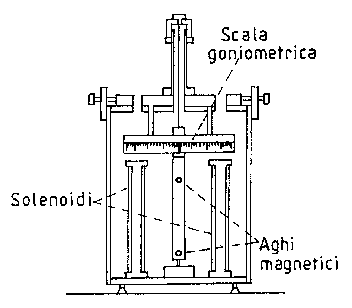
Fig.7.1. Magnetometro astatico e suo schema
Per la nostra esperienza avevamo a disposizione un magnetometro astatico raffigurato in fig.7.1. La condizione di astaticità è ottenuta collegando rigidamente due aghi magnetici uguali con orientazioni opposte.
| MAGNETI PERMANENTI | ||
lm |
Lm |
s(Lm) |
m |
m |
m |
0,06 |
0,2 |
0,0005 |
Dove L è la distanza tra i due aghi magnetici, ed l la lunghezza dell’ago magnetico.
L’apparato è composto da un equipaggio mobile, solenoidi e goniometro, tutti racchiusi in una custodia di modo che l’esterno non interagisca con le nostre misure.
Il principio di funzionamento del magnetometro astatico si basa sulla misurazione del momento meccanico di torsione di un filo di tungsteno dorato ricavando lo spostamento dalla posizione di equilibrio dell’equipaggio con gli aghi magnetici rispetto ai due solenoidi. Si legge la misura del doppio dell’angolo di deflessione su una scala goniometrica con un indice opportunamente tarato.
La precisione della taratura significa una maggior precisione nelle nostre misure, per cui abbiamo utilizzato tutti gli accorgimenti del caso.
La maggior difficoltà è stata riscontrata nel centraggio dell’equipaggio, cioè nella condizione in cui, inviando correnti concordi ai solenoidi, l’equipaggio mobile degli aghi magnetici non subisce deflessione. Per far sì che questa situazione fosse rispettata il piano formato degli aghi deve risultare perpendicolare a quello dei solenoidi (piano p nella fig.7.1.).
I solenoidi sono alimentati con correnti continue regolabili in intensità attraverso un potenziometro, misurate attraverso l’utilizzo di un tester amperometro.
I due solenoidi hanno le seguenti caratteristiche:
| SOLENOIDE | ||||
Ls |
Vs |
Ns |
R |
|
m |
m3 |
m |
||
0,304 |
0,000164 |
776 |
0,16 |
|
s(Ls) |
s(Vs) |
s(R) |
||
m |
m3 |
m |
||
0,0005 |
0,000001 |
0,005 |
||
Dove L è la lunghezza del solenoide, V il suo volume, N il numero delle spire ed R la distanza tra i due solenoidi.
Taratura del magnetometro astatico
Per la taratura dell’apparato di misura dell’intensità di magnetizzazione si alimentano i due solenoidi con correnti discordi. Ciascun solenoide equivale ad una barra magnetizzata con intensità di magnetizzazione
![]()
sapendo che la magnetizzazione è la
misura del momento magnetico all’unità di volume ricaviamo dalla fig.7.2. ![]() dove S è la sezione del solenoide.
dove S è la sezione del solenoide.
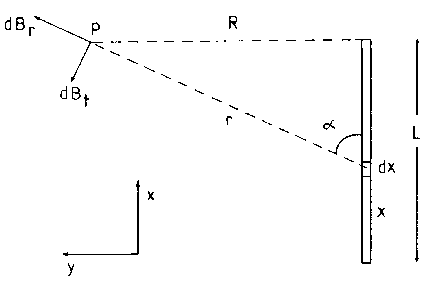
Fig.7.2. schema per il calcolo delle componenti del campo B generato da uno dei solenoidi uniformemente magnetizzato lungo l’asse x.
Integrando su tutto il solenoide L ponendo come ipotesi che sia uniformemente magnetizzato
![]()
da cui si ricava
![]()
nella condizione che Ls >>R
Il campo By nei punti in cui sono situati i due aghi magnetici è diretto in versi opposti, cosicchè i momenti meccanici agenti sull’equipaggio mobile sono concordi. La condizione di equilibrio dell’equipaggio mobile diventa:
![]()
dove m1 è il momento magnetico di ciascuno dei due aghi magnetici e q è l’angolo di cui è ruotato l’equipaggio.
Determiniamo la magnetizzazione
(*)![]()
dove C = mB0
La taratura del magnetometro ci fornisce il valore di K e la precisione è all’incirca dell’1%.
Conoscendo che
(**)![]()
si ricava il valore di K uguagliando le due equazioni asteriscate.
Nel nostro caso la condizione Ls>>R non è rispettata, come si vede dalla nostra tabella precedente, quindi dobbiamo tenere conto delle dimensioni geometriche dei solenoidi e degli aghi magnetici
| AGHI MAGENTICI PERMANENTI | ||
lm |
Lm |
s(Lm) |
m |
m |
m |
0,06 |
0,2 |
0,0005 |
Per calcolare il campo magnetico generato dal solenoide ai poli dell’ago magnetico quando quest’ultimo è ruotato di una angolo q rispetto alla posizione di riferimento. Assumendo che le masse magnetiche ai poli del solenoide abbiano un’azione trascurabile rispetto all’ago più lontano, troviamo il seguente campo nei rispettivi due poli magnetici:
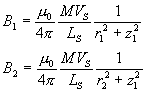
dove r1 e r2 sono le distanze dei due poli dall’asse del solenoide:

Troviamo il il momento meccanico agente sull’ago magnetico (ciascuno con momento magnetico m0 ) dovuto al campo magnetico generato dal solenoide esprimendo i campi magnetici giacenti nel piano normale all’asse dell’equipaggio mobile, che lo fanno deviare interagendo con il momento di dipolo degli aghi, e dopo una serie di conti ricaviamo:
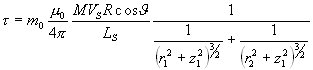
Troviamo la condizione di equilibrio tra il momento meccanico ed il momento di richiamo del filo elastico al quale è sospeso l’ago magnetico:
![]()
e si arriva alla conclusione che, tenendo conto anche del fatto che i solenoidi in realtà sono due, la magnetizzazione del solenoide è data da:
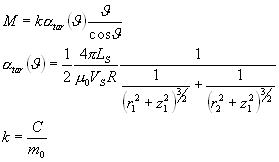
Il valore del coefficiente k si determina,
prendendo sempre ![]() , dalla pendenza della
miglior retta che passa per i nostri punti sperimentali attraverso il metodo dei minimi
quadrati applicato all’equazione:
, dalla pendenza della
miglior retta che passa per i nostri punti sperimentali attraverso il metodo dei minimi
quadrati applicato all’equazione:
![]()
A causa della presenza di materiale ferroso (calorifero) a destra dell’apparato utilizzato abbiamo deciso di stimare due valori del coefficiente k distinguendoli con ksinistra e kdestra che applicheremo alle rispettive misure condotte in seguito.
Determinazione del coefficiente ksinistra
I |
2qsinistra |
qsinistra |
mA |
gradi |
rad |
0,0 |
0,00 |
0,000000 |
20,2 |
12,75 |
0,111265 |
40,0 |
24,75 |
0,215984 |
60,4 |
36,50 |
0,318523 |
80,2 |
47,25 |
0,412334 |
100,2 |
57,75 |
0,503964 |
119,6 |
66,75 |
0,582504 |
139,9 |
75,50 |
0,658862 |
159,9 |
83,00 |
0,724312 |
180,3 |
90,00 |
0,785398 |
198,2 |
95,50 |
0,833395 |
Da questi dati sperimentali
z1 |
r21 |
r22 |
atar(q) |
atar(q)*q/cos(q) |
M sol |
rad |
Asp/m |
||||
0,052 |
0,0265 |
0,0265 |
144548394 |
0 |
4,491110925 |
0,0254341 |
0,027566 |
134601047 |
15069533,5 |
54,0857749 |
|
0,0244426 |
0,028557 |
134465829 |
29733362,7 |
102,3452436 |
|
0,0234936 |
0,029506 |
133738826 |
44855087 |
152,1116701 |
|
0,0226528 |
0,030347 |
132610845 |
59682038,5 |
200,9079835 |
|
0,0218642 |
0,031136 |
131145971 |
75476404,9 |
252,8881124 |
|
0,0212189 |
0,031781 |
129660023 |
90442488,9 |
302,1423182 |
|
0,0206227 |
0,032377 |
128062207 |
106711026 |
355,6829681 |
|
0,0201388 |
0,032861 |
126609990 |
122443940 |
407,4608549 |
|
0,0197118 |
0,033288 |
125215063 |
139078967 |
462,2076448 |
|
0,0193939 |
0,033606 |
124109301 |
153832752 |
510,7631607 |
Abbiamo trovato i valori di fit della magnetizzazione del solenoide e dalla miglior retta

Abbiamo risolto il valore di ksinistra come
K sinistra |
s(K) |
3,291E-06 |
2,4E-09 |
Con un ottimo grado di aprossimazione
Stessa cosa per kdestra
Determinazione del coefficiente kdestra
I |
2qdestra |
qdestra |
mA |
gradi |
rad |
0,0 |
-0,75 |
-0,00654 |
19,9 |
13,00 |
0,113446 |
39,8 |
26,75 |
0,233438 |
60,7 |
41,50 |
0,362156 |
80,2 |
55,25 |
0,482147 |
99,5 |
67,75 |
0,59123 |
119,0 |
80,75 |
0,704677 |
139,6 |
92,25 |
0,805033 |
160,3 |
102,00 |
0,890118 |
179,3 |
109,00 |
0,951204 |
198,0 |
115,50 |
1,007928 |
atar(q) |
atar(q)*q/cos(q) |
M sol |
rad |
Asp/m |
|
144547140 |
-946079,1 |
24,43681 |
124551291 |
14221312 |
62,83117 |
123306231 |
29586820 |
101,727 |
121121363 |
46907448 |
145,572 |
118438838 |
64452447 |
189,985 |
115609866 |
82326523 |
235,231 |
112437149 |
104003216 |
290,1029 |
109570446 |
127267993 |
348,9947 |
107186481 |
151605778 |
410,6028 |
105541290 |
172878997 |
464,4533 |
104086226 |
196605192 |
524,5132 |
Da cui:

Si trova
K destra |
s(K) |
2,531E-06 |
8,9E-09 |
Misura della curva di magnetizzazione dell’acciaio magnetico
Per compiere questa misura si introduce in uno dei due solenoidi una barra cilindrica della sostanza debolmente magnetizzata che ha una lunghezza uguale a quella della distanza tra i due aghi magnetici. Siamo stati attenti ad appendere all’interno del solenoide questa barra alla medesima altezza dell’equipaggio mobile.
| ACCIAIO MAGNETICO | ||
Lh=Lm |
Vh |
|
m |
m3 |
|
0,2 |
2,51327E-06 |
|
s(Lh) |
dmagn |
s(d) |
m |
mm |
mm |
0,0001 |
4,00 |
0,05 |
Determiniamo la curva di magnetizzazione tra i valori 0 < M < Mr alimentando i solenoidi con correnti concordi in modo tale che l’equipaggio senza la barra non subisca deflessioni apprezzabili. Una piccola deflessione è dovuta alla magnetizzazione residua non uguale dei due solenoidi.
Introducendo la barra inizialmente con corrente nulla si determina una deflessione angolare dell’equipaggio mobile dovuto alla magnetizzazione residua della barra introdotta.
Conoscendo che il valore di campo magnetico H è
(*)![]()
ed utilizzando sempre l’equazione che descrive la magnetizzazione:
![]()
ma con un valore di
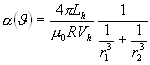
arriviamo alla conclusione che
(**)![]()
Utilizziamo il coefficiente k destro per le nostre misure.
I |
2q |
q |
mA |
gradi |
rad |
0,0 |
142,50 |
1,243547 |
19,8 |
137,75 |
1,202096 |
40,5 |
131,75 |
1,149736 |
59,6 |
122,25 |
1,066833 |
78,8 |
100,75 |
0,87921 |
84,2 |
75,50 |
0,658862 |
86,9 |
72,25 |
0,6305 |
89,9 |
61,25 |
0,534507 |
94,3 |
41,00 |
0,357792 |
98,1 |
25,00 |
0,218166 |
100,6 |
15,75 |
0,137445 |
102,7 |
7,25 |
0,063268 |
103,0 |
-0,25 |
-0,002182 |
atar(q) |
atar(q)q/cosq |
a(q) |
M sol (q) |
H |
M (q) |
Asp/m |
Asp/m |
Asp/m |
|||
119681438 |
463009434 |
8512509548 |
1198,882301 |
0 |
85272,18 |
99859344 |
333072106 |
8573913610 |
869,9621692 |
50,5421053 |
74694,87 |
100864772 |
283728100 |
8660239566 |
745,0539753 |
103,381579 |
63970,26 |
102667947 |
226815956 |
8815060014 |
600,9879832 |
152,136842 |
51600,77 |
107487124 |
148180653 |
9228834068 |
401,9325255 |
201,147368 |
34509,89 |
113736004 |
94773359,6 |
9765362301 |
266,738627 |
214,931579 |
22902,15 |
114529762 |
89399667,5 |
9833514284 |
253,135796 |
221,823684 |
21734,22 |
117117883 |
72747118,2 |
1,0056E+10 |
210,9819452 |
229,481579 |
18114,89 |
121208204 |
46299427,2 |
1,0407E+10 |
144,0329156 |
240,713158 |
12366,65 |
123509613 |
27599844 |
1,0605E+10 |
96,69725411 |
250,413158 |
8302,417 |
124368559 |
17256537,1 |
1,0678E+10 |
70,51446329 |
256,794737 |
6054,365 |
124822045 |
7913096,5 |
1,0717E+10 |
46,86270923 |
262,155263 |
4023,628 |
124944765 |
-272587,84 |
1,0728E+10 |
26,14167072 |
262,921053 |
2244,521 |
dalle equazioni asteriscate ricaviamo la curva di magnetizzazione
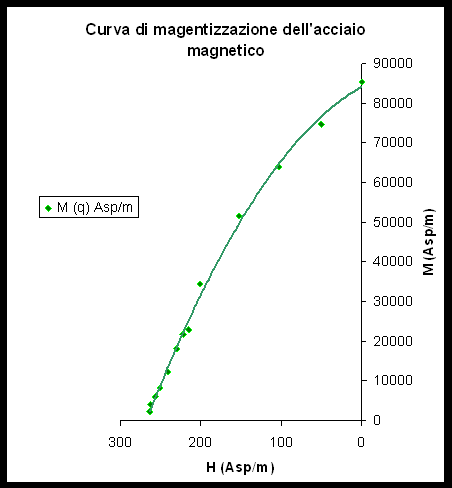
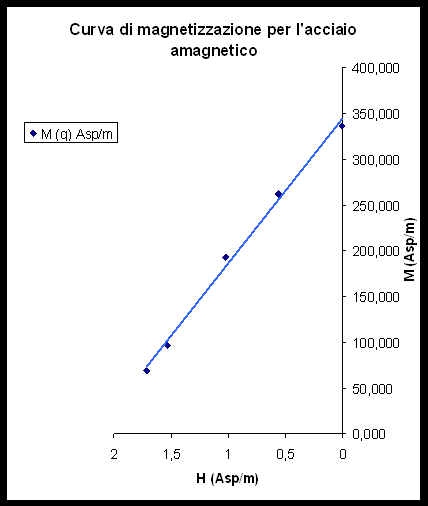
Misura della curva di magnetizzazione dell’acciaio amagnetico
Procediamo sempre nel medesimo modo della prima misura, solo che questa volta utilizziamo il coefficiente k sinistra.
Introduciamo questa seconda barra in uno dei due solenoidi e misuriamo la deflessione dell’equipaggio mobile in funzione della corrente di alimentazione dei solenoidi.
In questo caso abbiamo misurato bene la posizione di zero dello strumento (in assenza della barra) e con corrente massima nei due solenoidi ed abbiamo trovato:
I |
2q |
q |
A |
gradi |
rad |
2,00 |
0,00 |
0,00 |
| (senza la barra) | ||
Ci proponiamo qui di determinare attraverso la solita equazione
![]()
ed in relazione alle dimensioni della barra
| ACCIAIO AMAGNETICO | ||
Lb=Lm |
Vb |
|
m |
m3 |
|
0,2 |
1,403E-05 |
|
s(Lb) |
damagn |
s(d) |
m |
mm |
mm |
0,0005 |
9,45 |
0,05 |
Con i seguenti dati sperimentali
I |
2q |
q |
A |
gradi |
rad |
0,00 |
5,00 |
0,0436332 |
0,22 |
3,50 |
0,0305433 |
0,40 |
2,25 |
0,0196350 |
0,60 |
0,50 |
0,0043633 |
0,67 |
0,00 |
0,0000000 |
Abbiamo determinato
| X | Y | FIT |
|||||
atar(q) |
atar(q)*q/cos(q) |
a(q) |
M sol (q) |
H |
M (q) |
M (q)fit |
|
rad |
Asp/m |
Asp/m |
Asp/m |
Asp/m |
|||
144492678 |
6310688,82 |
1921153153 |
25,260 |
0 |
335,852 |
344,349 |
|
124916241 |
3817129,8 |
1921611845 |
17,053 |
0,562 |
262,337 |
255,362 |
|
124933060 |
2453527,84 |
1921870581 |
12,566 |
1,021 |
193,302 |
182,555 |
|
124944326 |
545177,656 |
1922043886 |
6,285 |
1,532 |
96,688 |
101,658 |
|
124944911 |
0 |
1922052890 |
4,491 |
1,710 |
69,088 |
73,344 |
|
E usando il metodo dei minimi quadrati applicato a
![]()
abbiamo risolto la suscettività magnetica e la permeabilità magnetica relativa nei rispettivi valori:
c |
s(c) |
mr |
-158,5 |
1,8 |
-157,458 |
Ci possiamo ritenere soddisfatti delle nostre misurazioni, anche se ci permettiamo di fare una piccola osservazione sulla posizione del tavolo dell’esperimento troppo vicino al calorifero, materiale ferroso, che amplifica la differenza tra i valori di k misurati a sinistra e a destra dell’apparato sperimentale. Se avessimo potuto fare una media dei due valori di k avremmo ottenuto risultati maggiormente affidabili.