6. MISURE ELETTRICHE IN CIRCUITI A CORRENTE ALTERNATA
Scopo dell’esperienza
Ci proponiamo di misurare
Descrizione dell’esperimento e analisi dei dati
Misura delle resistenze, delle reattanze induttive e delle reattanze capacitive
Abbiamo a nostra disposizione cinque resistenze, quattro induttori e cinque capacitori incogniti. Realizziamo i circuiti contenti il generatore in corrente alternata e immettiamo, una alla volta, le impedenze da determinare a diversi valori di frequenza della forza elettromotrice f.e.m. Misuriamo la frequenza utilizzando un frequenzimetro.
Abbiamo a disposizione due tester che misurano ai capi delle induttanze la tensione Vefficace e la corrente Iefficace . Utilizziamo perciò il metodo voltamperometrico.
![]()
Abbiamo proceduto come segue per la determinazione delle cinque resistenze:
n |
I eff |
V eff |
Z=R |
<R> |
s(R) |
|
Hz |
mA |
V |
W |
W |
W |
|
| 1 circuito | 25 |
0,744 |
7,37 |
9906 |
9941,43 |
29,51 |
550 |
0,735 |
7,29 |
9918 |
|||
1131 |
0,730 |
7,30 |
10000 |
|||
| 2 circuito | 25 |
61,9 |
3,55 |
57 |
57,56 |
0,18 |
550 |
61,3 |
3,52 |
57 |
|||
1131 |
61,3 |
3,55 |
58 |
|||
| 3 circuito | 25 |
27,7 |
5,7 |
206 |
206,56 |
0,75 |
550 |
27,4 |
5,64 |
206 |
|||
1131 |
27,3 |
5,68 |
208 |
|||
| 4 circuito | 25 |
45,7 |
4,56 |
100 |
100,15 |
0,27 |
550 |
45,2 |
4,52 |
100 |
|||
1131 |
45,2 |
4,55 |
101 |
|||
| 5 circuito | 25 |
102,4 |
0,99 |
10 |
9,74 |
0,04 |
550 |
101,6 |
0,99 |
10 |
|||
1131 |
102 |
1 |
10 |
Abbiamo voluto determinare approssimativamente l’andamento della R al variare della frequenza:
n |
R1 |
R2 |
R3 |
R4 |
R5 |
HZ |
OHM |
OHM |
OHM |
OHM |
OHM |
25 |
9906 |
57 |
206 |
100 |
10 |
550 |
9918 |
57 |
206 |
100 |
10 |
1131 |
10000 |
58 |
208 |
101 |
10 |

Ed abbiamo constatato che la resistenza non dipende dalla frequenza. Infatti sappiamo per la leggi di Ohm V=RI che si ha Z = R.
Per i capacitori abbiamo svolto le stesse procedure:
n |
I eff |
V eff |
Z=1/wC |
C |
<C> |
s(<C>) |
||
Hz |
MA |
V |
W |
nF |
nF |
nF |
||
| 1 circuito | 23 |
0,49 |
7,48 |
15265 |
453 |
464 |
4 |
|
50 |
0,86 |
5,91 |
6872 |
463 |
||||
216 |
4,740 |
7,37 |
1555 |
474 |
||||
845 |
17,91 |
7,26 |
405 |
465 |
||||
| 2 circuito | 23 |
0,506 |
7,48 |
14783 |
468 |
484 |
6 |
|
50 |
0,92 |
5,91 |
6424 |
496 |
||||
216 |
4,92 |
7,37 |
1498 |
492 |
||||
845 |
18,57 |
7,26 |
391 |
482 |
||||
| 3 circuito | 23 |
0,215 |
7,48 |
34791 |
199 |
205 |
4 |
|
50 |
0,37 |
5,91 |
15973 |
199 |
||||
216 |
2,1 |
7,37 |
3510 |
210 |
||||
845 |
8,2 |
7,26 |
885 |
213 |
||||
| 4 circuito | 23 |
0,101 |
7,48 |
74059 |
93 |
97 |
3 |
|
50 |
0,17 |
5,91 |
34765 |
92 |
||||
216 |
1 |
7,37 |
7370 |
100 |
||||
845 |
3,94 |
7,26 |
1843 |
102 |
||||
| 5 circuito | 23 |
0,05 |
7,48 |
149600 |
46,3 |
48,9 |
1 |
|
50 |
0,094 |
5,91 |
62872 |
50,6 |
||||
216 |
0,49 |
7,37 |
15041 |
49,0 |
||||
845 |
1,92 |
7,26 |
3781 |
49,8 |
||||
Ed abbiamo cercato di determinare come si comporta la capacità in funzione della frequenza utilizzata. Dalle leggi di Ohm ricaviamo che il capacitore è in relazione con la frequenza in questi termini:
![]()
dalla quale ricaviamo i seguenti dati e la misura delle diverse capacità dallo studio della pendenza della miglior retta con il metodo dei minimi quadrati
| frequenza^2 | (I^2/V^2)1 |
(I^2/V^2)2 |
(I^2/V^2)3 |
(I^2/V^2)4 |
(I^2/V^2)5 |
rad^2 |
A^2/V^2 |
A^2/V^2 |
A^2/V^2 |
A^2/V^2 |
A^2/V^2 |
20884,08 |
4,29E-09 |
4,58E-09 |
8,26E-10 |
1,82E-10 |
4,46824E-11 |
98696,04 |
2,12E-08 |
2,42E-08 |
3,92E-09 |
8,27E-10 |
2,52977E-10 |
1841905 |
4,14E-07 |
4,46E-07 |
8,12E-08 |
1,84E-08 |
4,42036E-09 |
28188577 |
6,09E-06 |
6,54E-06 |
1,28E-06 |
2,95E-07 |
6,99406E-08 |
C1 |
C2 |
C3 |
C4 |
C5 |
|
nF |
nF |
nF |
nF |
nF |
|
464,5 |
481,6 |
212,8 |
102,3 |
49,8 |
Come possiamo osservare i valori delle capacità determinati dalla pendenza della curva di fit sono molto simili a quelle determinate con il solo utilizzo dei dati sperimentali.

Appuriamo anche dal grafico che la capacità dipende dalla frequenza, infatti sappiamo che Z= -i/w C.
Per le induttanze abbiamo trovato i seguenti valori:
n |
I eff |
V eff |
Z=wL |
L |
<L> |
s (<L>) |
|
Hz |
MA |
V |
W |
H |
H |
H |
|
| 1 circuito | 23 |
23,7 |
7,2 |
304 |
2,1 |
1,9 |
0,1 |
50 |
9,6 |
5,83 |
607 |
1,9 |
|||
216 |
2,45 |
5,88 |
2400 |
1,8 |
|||
845 |
0,65 |
5,95 |
9154 |
1,7 |
|||
| 2 circuito | 23 |
23,7 |
7,2 |
304 |
2,1 |
1,9 |
0,1 |
50 |
9,73 |
5,84 |
600 |
1,9 |
|||
216 |
2,47 |
5,88 |
2381 |
1,8 |
|||
845 |
0,65 |
5,95 |
9154 |
1,7 |
|||
| 3 circuito | 23 |
99,5 |
3,59 |
36 |
0,25 |
0,23 |
0,01 |
50 |
60 |
4,53 |
76 |
0,24 |
|||
216 |
18,2 |
5,7 |
313 |
0,23 |
|||
845 |
5,26 |
5,88 |
1118 |
0,21 |
|||
| 4 circuito | 23 |
100 |
3,53 |
35 |
0,24 |
0,23 |
0,01 |
50 |
60,8 |
4,5 |
74 |
0,24 |
|||
216 |
18,6 |
5,71 |
307 |
0,23 |
|||
845 |
5,39 |
5,87 |
1089 |
0,21 |
Cercando sempre di determinare un andamento dell’induttanza in funzione della frequenza applicando le leggi di Ohm troviamo:
![]()
dalla quale ricaviamo i seguenti dati e la misura delle diverse induttanze dallo studio della pendenza della miglior retta con il metodo dei minimi quadrati:
| frequenza^2 | (V^2/I^2)1 | (V^2/I^2)2 | (V^2/I^2)3 | (V^2/I^2)4 |
| rad^2 | V^2/A^2 | V^2/A^2 | V^2/A^2 | V^2/A^2 |
20884,08 |
92292,9 |
92292,9 |
1301,795 |
1246,09 |
98696,04 |
368803,2 |
360246,7 |
5700,25 |
5477,948 |
1841905 |
5760000 |
5667098 |
98085,98 |
94242,4 |
28188577 |
83792899 |
83792899 |
1249635 |
1186038 |
iL1 |
iL2 |
iL3 |
iL4 |
|
H |
H |
H |
H |
|
1,7229 |
1,7232 |
0,210 |
0,205 |
Ed anche qui riscontriamo una buona approssimazione con i risultati sperimentali.

Anche da questo grafico possiamo rilevare che l’induttanza dipende dalla frequenza, infatti sappiamo che Z= iw L.
Misura del valore di impedenza per i circuiti RLC in serie.
 Fig.6.1.
Circuiti RLC in serie
Fig.6.1.
Circuiti RLC in serie
Vogliamo misurare, sempre servendoci del metodo voltamperometrico i valori dell’impedenza totale del circuito. Abbiamo inserito nel circuito la prima resistenza, il primo capacitore e la prima induttanza della parte precedente.
n |
I eff |
V eff |
Ztot |
Z(th) |
Hz |
mA |
V |
W |
W |
23 |
0,3 |
5,95 |
19833 |
17963 |
50 |
0,47 |
5,92 |
12596 |
11751 |
216 |
0,55 |
5,87 |
10673 |
9977 |
845 |
0,41 |
5,87 |
14317 |
13243 |
Dove Ieff e Veff
sono i valori rispettivamente della corrente e della tensione corretti di un fattore ![]() .
.
Z totale è l’impedenza misurata sperimentalmente, mentre Z th è l’impedenza misurata attraverso i valori di impedenze già conosciuti:
![]()

Come si può vedere le misure sperimentali concordano bene con la teoria con un valore di probabilità del c 2 vicino al 37%.
Misura dell’angolo di sfasamento
Metodo dei fasori
Abbiamo misurato la tensione efficace ai capi di ciascuna impedenza del nostro circuito RLC di fig.6.1. ed abbiamo riportato le nostre misure nel piano complesso.
L’intensità di corrente è uguale all’interno di ciascuna impedenza per cui può essere rappresentata da un vettore sull’asse reale. Le tensioni dei vari elementi del circuito sono:
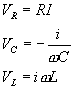
La somma vettoriale dei fasori rappresenta secondo la legge di Kirchhoff, la f.e.m. del generatore:
![]()
l’angolo f compreso tra il vettore risultante V tot e l’asse reale rappresenta l’angolo di sfasamento, e sapendo che
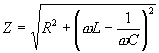
otteniamo la seguente relazione
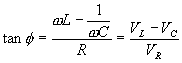
dalla quale possiamo calcolare l’angolo di sfasamento:
n |
V(R) |
V(C) |
V(L) |
f |
Hz |
V |
V |
V |
rad |
23 |
3,25 |
4,9 |
0,071 |
-0,98 |
50 |
4,81 |
3,44 |
0,22 |
-0,59 |
216 |
5,74 |
1,03 |
1,24 |
0,04 |
845 |
4,32 |
0,2 |
3,51 |
0,65 |
Metodo dell’ellisse
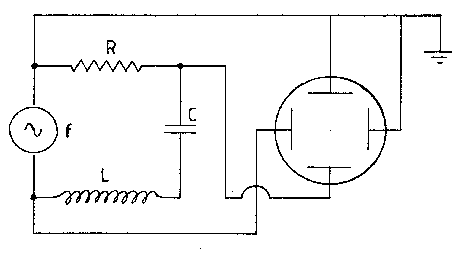 Fig.6.2.
Schema dei collegamenti all’oscilloscopio per la misura dell’angolo di
sfasamento del circuito RLC in serie.
Fig.6.2.
Schema dei collegamenti all’oscilloscopio per la misura dell’angolo di
sfasamento del circuito RLC in serie.
Per la misura dell’angolo di sfasamento abbiamo a disposizione un oscilloscopio a doppia traccia a cui inviamo i segnali di tensione prelevati ai capi del generatore e ai capi di un elemento posto in serie al generatore del circuito. Il segnale di tensione del generatore, inviato al primo connettore dell’oscilloscopio a doppia traccia, viene utilizzato per la deflessione orizzontale di elettroni, mentre il segnale proveniente dall’elemento resistivo, inviato al secondo connettore verticale dell’oscilloscopio, comanda la deflessione verticale del fascio di elettroni. I due segnali producono degli spostamenti della traccia sullo schermo dell’oscilloscopio esprimibile con le seguenti relazioni:
![]()
Sviluppando l’ultima espressione ed effettuando le opportune sostituzioni si ricava l’equazione dell’ellisse:
![]()
Osserviamo che l’ellisse diventa una circonferenza se i segnali hanno la stessa ampiezza (a = b) e sono sfasati di p /2 o 3p /2. L’ellisse diventa una retta quando lo sfasamento è f =0 oppure p . La traccia dell’ellisse sullo schermo non cambia orientamento variando la fase al valore positivo di +f al valore negativo di -f . Ne consegue che nella misura dell’angolo di sfasamento con il metodo dell’ellisse si ha un’indeterminazione sul segno dello sfasamento.
Per determinare l’angolo di sfasamento si procede come da fig.6.3.: abbiamo misurato la massima estensione verticale dell’ellisse AB e la larghezza dell’ellisse per x=0 CD.
Per la determinazione di queste lunghezze abbiamo cercato di far combaciare il più possibile i punti da misurare con la maschera del reticolo di misura.
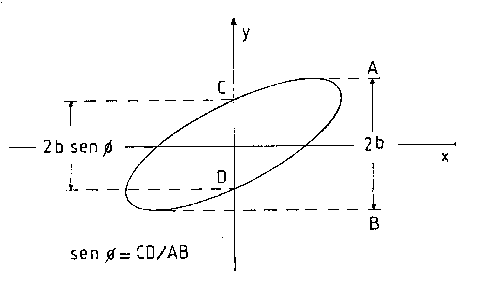 Fig.6.3.
Caratteristiche dell’ellisse prodotta all’oscilloscopio da due segnali di
tensione sfasati di un angolo f
Fig.6.3.
Caratteristiche dell’ellisse prodotta all’oscilloscopio da due segnali di
tensione sfasati di un angolo f
In questo modo siamo giunti alla conclusione che
![]()
da cui si ricavano i seguenti valori per l’angolo di sfasamento:
n |
AB |
CD |
f |
Hz |
rad |
||
23 |
1,8 |
1,4 |
0,89 |
50 |
2,4 |
1,4 |
0,62 |
216 |
prossimo alla risonanza | ||
845 |
2,4 |
1,5 |
0,68 |
Per i valori di frequenza prossimi alla risonanza non siamo potuti risalire ai valori di AB e CD poiché l’ellisse risultava degenere al punto da assomigliare ad una retta.
Questi sono all’incirca gli stessi risultati ottenuti con il metodo dei fasori. In questo metodo concorrono però molte cause di errore fra cui la difficoltà di misurare i segmenti AB e CD stimando di volta in volta, al variare della frequenza, la giusta posizione e misura della massima lunghezza AB. Il metodo dei fasori può essere considerato il più affidabile per la precisione nella misurazione della tensione grazie ai tester posti ai capi delle impedenze.
Determinazione della frequenza di risonanza
Vogliamo determinare la condizione in cui il circuito RLC in serie diventa puramente resistivo. La tensione misurata ai capi della resistenza R presenta un massimo (al variare della f.e.m. alternata) quando si raggiunge la condizione di risonanza:
![]()
dalla quale possiamo ricavare il valore della frequenza w th:
w(sp) |
w(th) |
Hz |
Hz |
193,67 |
170,36 |
che è simile a quello determinato sperimentalmente w sp .
Dato che il generatore di funzioni d’onda non è stabilizzato, la f.e.m. da esso fornita non rimane costante al variare della frequenza, per cui sarebbe stato necessario misurare contemporaneamente sia la tensione efficace della resistenza V(R) che la tensione efficace del generatore (f0), cosa che non è stata possibile perché aggiungendo i tester per la misurazione delle tensioni delle impedenze si destabilizzava il generatore.
Riportiamo il grafico del rapporto V(R)/ f0 in funzione della frequenza.
n |
V(R)/f0 |
V(R)/f0 |
Hz |
sperimentale |
teorico |
23 |
0,395329 |
0,561537 |
50 |
0,567887 |
0,845731 |
216 |
0,716604 |
0,995319 |
845 |
0,537983 |
0,71987 |
V(R)/ f0 teorico è dato da
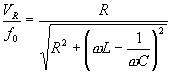
mentre V(R)/ f0 sperimentale è dato dai dati sperimentali trovati in precedenza.
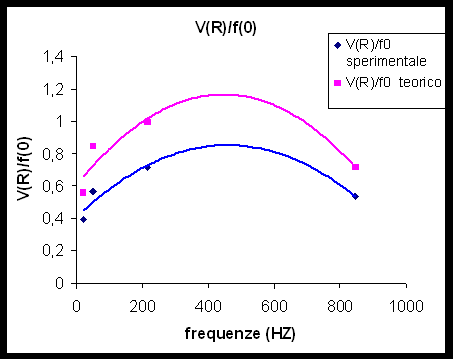
Anche se i dati sono in numero troppo esiguo per la determinazione di una curva di fit tramite il metodo dei minimi quadrati possiamo ugualmente osservare come le due funzioni si assomiglino e presentino un massimo laddove è soddisfatta la condizione di risonanza che, ribadiamo, non si può determinare in modo soddisfacente dal grafico che ha solo un valore indicativo.