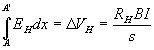
5. MISURE DI CAMPO MAGNETICO
CARATTERISTICA DELL’ELETTROMAGNETE.
Lo scopo dell’esperienza consiste nella misura del campo di induzione magnetica B nel piano mediano delle espansioni polari di un elettromagnete utilizzando una sonda di Hall. Si tratta di determinare la caratteristica B= B(I) dell’elettromagnete e l’andamento del campo magnetico di fuga.
CENNI DI TEORIA
Assumendo che il flusso del campo B rimanga confinato sia nella regione delle espansioni polari e del giogo (flusso disperso nullo), sia nella regione del traferro (campo di fuga nullo), si può applicare il teorema di Ampere lungo una generica linea di forza nel seguente modo:
H1 l 1+H2 l2 +....+Hnln=NI
dove H1 ,......Hn sono i valori costanti in modulo del campo magnetico nelle diverse sezioni dell’elettromagnete le cui lunghezze sono rispettivamente l1,....ln.
Le condizioni di flusso disperso nullo e di campo di fuga nullo permettono di scrivere le relazioni:
H1=f (B)/m 11S1 H2=f (B)/m n1Sn
Sostituendo queste relazioni nell’espressione precedente si ottiene:
f (B)[l1/m 1S1 +....+ln/m n1Sn]=NI
Agli addenti nella quadra si dà il nome di riluttanze del circuito magnetico.La riluttanza relativa al traferro rappresenta la componente più importante della riluttanza globale dell’elettromagnete. Infatti anche se l’apertura del traferro è piccola, la permeabilità del vuoto risulta notevolmente inferiore a quella del ferro, tipicamente si ha: m Fe / m 0 >1000
Per un magnete ad H come quello da noi usato in laboratorio la relazione trovata in precedenza si può riscrivere:
f (B)[h/m 0Sp+Lp/m rm 0Sp + Lg/2m rm 0Sg]=NI
dove Sp e Sg sono le sezioni dell’espansione polare e del giogo, h, Lp ed Lg sono l’apertura del traferro e la lunghezza di una linea mediana nei poli e nel giogo. Trascurando il flusso disperso, la riluttanza del traferro risulta costante a tutti i livelli di campo; inoltre avendo utilizzato un magnete di ferro Armco a basso tenore di carbonio e avendo prodotto un campo magnetico inferiore a 1.5 T, abbiamo potuto trascurare la riluttanza del traferro semplificando ulteriormente l’espressione:
Bh/m 0=NI
Da quest’ultima espressione risulta chiara la dipendenza lineare che intercorre tra I e B. La prima parte dell’esperimento consiste nel ricavare la costante di proporzionalità k (B=kI). Per effettuare questa misura abbiamo utilizzato una sonda di Hall che ci ha consentito di valutare il campo magnetico dell’elettromagnete essendo nota la corrente passante nelle spire. La sonda di Hall si basa su un fenomeno galvanomagnetico per il quale si produce un campo elettromotore E tra due estremità di un a lamina conduttrice posta in un campo magnetico B normale alla lamina stessa quando quest’ultima è percorsa da una corrente elettrica in direzione ortogonale sia a E che a B. Dalla misura della forza elettromotrice tra i due punti opposti A ed A’ della lamina si ricava:
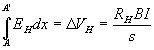
In questo modo avendo misurato la differenza di potenziale tramite un voltmetro, ed essendo noto il coefficiente di Hall K (K=RI/s), siamo stati in grado di calcolare il campo magnetico nei punti interni ed esterni al traferro.
ANALISI DEI DATI.
La misura è stata eseguita dapprima aumentando la corrente fino al valore massimo consentito dalla strumentazione di laboratorio (4 A) ed in seguito diminuendo la corrente fino a zero registrando i valori di corrente e di campo magnetico ad intervalli regolari (0.25 A):
traferro h = 12 mm spire N = 630
larghezza dei poli x = 50 mm superficie poli Sp = 5000 mm
lunghezza dei poli y = 100 mm altezza poli Lp = 54 mm
spessore del giogo = 25 mm K (Hall) = 6.087 mV/kG
I D V B I D V B
A mV KG A mV KG
0 0.070 0.011 0 0.22 0.036
0 0.192 0.032 0.25 1.119 0.184
0.25 1.041 0.171 0.5 2.15 0.353
0.5 1.963 0.322 0.75 3.085 0.507
0.75 3.004 0.494 1 4.064 0.668
1 4.015 0.660 1.25 5.032 0.827
1.25 5.171 0.850 1.5 6.078 0.999
1.5 6.026 0.990 1.75 7.02 1.153
1.75 7.049 1.158 2 8.125 1.335
2 8.078 1.327 2.25 9.075 1.491
2.25 9.161 1.505 2.5 10.14 1.666
2.5 10.1 1.659 2.75 11.125 1.828
2.75 11.15 1.832 3 12.16 1.998
3 12.11 1.989 3.25 13.12 2.155
3.25 13.18 2.165 3.5 14.212 2.335
3.5 14.194 2.332 3.75 15.113 2.483
3.75 15.215 2.500 4 16.203 2.662
4 16.411 2.696 3.75 15.264 2.508
3.75 15.312 2.516 3.5 14.42 2.369
3.5 14.454 2.375 3.25 13.385 2.199
3.25 13.408 2.203 3 12.499 2.053
3 12.329 2.025 2.75 11.398 1.873
2.75 11.382 1.870 2.5 10.468 1.720
2.5 10.444 1.716 2.25 9.426 1.549
2.25 9.43 1.549 2 8.38 1.377
2 8.41 1.382 1.75 7.312 1.201
1.75 7.359 1.209 1.5 6.309 1.036
1.5 6.673 1.096 1.25 5.243 0.861
1.25 5.3 0.871 1 4.307 0.708
1 4.301 0.707 0.75 3.291 0.541
0.75 3.313 0.544 0.5 2.229 0.366
0.5 2.251 0.370 0.25 1.162 0.191
0.25 1.171 0.192 0 0.232 0.038
Il fit dei dati sperimentali riportati nella tabella sopra ha fornito i seguenti risultati per il coefficiente di linearità k:
ksp = 0.6637 ± 0.0262 kG/A
b = 0.0248 ± 0.0066 kG (intercetta)
Il confronto con il valore teorico k’ = m 0 * N/h = 0.6597 è soddisfacente, infatti tale valore è pienamente compreso nella barra di errore ottenuta sperimentalmente, inoltre il set di dati ottenuti è abbastanza buono: c 2 = 26.55 %
Confrontiamo ora il valore teorico della riluttanza del ferro, ottenuto con misure geometriche, con il valore della riluttanza del traferro :riluttanza traferro = h/m 0 Sp =1.910 x 106 A2/ N m
riluttanza ferro = Lp/m r m 0 Sp =4.297 x 103 A2/ N m
Questi dati giustificano la scelta di trascurare la riluttanza del ferro nel calcolo svolto in precedenza.
CAMPO DI FUGA.
CENNI DI TEORIA.
L’ipotesi che il campo d’induzione magnetica B sia costante e confinato nella regione del traferro delimitata dalle espansioni polari introduce un’approssimazione troppo drastica nel calcolo della caratteristica di un elettromagnete. Il flusso infatti non rimane confinato nella regione delimitata dalle superfici laterali delle espansioni polari.
Un parametro che serve a descrivere in maniera integrale l’effetto del campo di fuga è la lunghezza fisica del polo:
![]()
dove B0 è il valore del campo sull’asse delle espansioni polari al centro del magnete,
Tale parametro rappresenta la lunghezza di un magnete ideale in cui il campo d’induzione magnetica assume il valore costante B = B0 sino al bordo del magnete e al di fuori delle espansioni polari assume il valore B=0. Nel caso di un polo a sezione rettangolare è utile la definizione di sezione fisica:
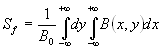
il flusso reale del campo vale:
![]()
ANALISI DEI DATI.
L’esperienza consiste nella misura del campo B nel piano mediano dell’elettromagnete ai vertici di un reticolo cartesiano di passo: D x = 0.25cm D y = 0.5 cm. Per effettuare la mappatura abbiamo assunto un valore costante B0 =2.670 kG nella zona centrale del magnete ed abbiamo effettuato la mappatura in direzione x a partire dal centro del magnete e quella in direzione y a partire da 2.5 cm dal centro. I valori della differenza di potenziale D V (mV) rilevati sulla lamina della sonda di Hall sono riportati nella seguente tabella:
x (cm) |
||||||||
y (cm) |
0 |
0.25 |
0.5 |
0.75 |
1 |
1.25 |
1.5 |
1.75 |
2.5 |
16.251 |
16.247 |
16.243 |
16.218 |
16.166 |
16.022 |
16.003 |
15.805 |
3 |
16.244 |
16.247 |
16.236 |
16.198 |
16.163 |
16.016 |
15.983 |
15.780 |
3.5 |
16.242 |
16.232 |
16.216 |
16.197 |
16.142 |
15.991 |
15.977 |
15.779 |
4 |
16.228 |
16.216 |
16.201 |
16.154 |
16.122 |
15.991 |
15.952 |
15.779 |
4.5 |
14.996 |
14.974 |
14.954 |
14.934 |
14.882 |
14.734 |
14.709 |
14.516 |
5 |
6.661 |
6.655 |
6.641 |
6.602 |
6.527 |
6.416 |
6.331 |
6.145 |
5.5 |
3.130 |
3.121 |
3.116 |
3.074 |
3.024 |
2.931 |
2.869 |
2.786 |
6 |
1.611 |
1.595 |
1.590 |
1.571 |
1.536 |
1.491 |
1.456 |
1.405 |
6.5 |
0.808 |
0.798 |
0.797 |
0.772 |
0.768 |
0.751 |
0.728 |
0.703 |
7 |
0.391 |
0.389 |
0.387 |
0.386 |
0.369 |
0.360 |
0.359 |
0.345 |
2 |
2.25 |
2.5 |
2.75 |
3 |
3.25 |
3.5 |
3.75 |
4 |
15.159 |
13.792 |
11.069 |
9.119 |
7.184 |
5.717 |
4.591 |
3.726 |
3.017 |
15.180 |
13.678 |
11.042 |
9.058 |
7.128 |
5.711 |
4.571 |
3.695 |
2.975 |
15.119 |
13.648 |
11.025 |
8.993 |
7.060 |
5.620 |
4.518 |
3.632 |
2.956 |
15.093 |
13.647 |
10.986 |
8.851 |
7.022 |
5.560 |
4.427 |
3.560 |
2.871 |
13.787 |
12.305 |
9.844 |
7.829 |
6.244 |
4.887 |
3.882 |
3.111 |
2.513 |
5.842 |
5.453 |
4.874 |
4.452 |
3.746 |
3.170 |
2.663 |
2.237 |
1.854 |
2.655 |
2.509 |
2.349 |
2.193 |
1.991 |
1.782 |
1.575 |
1.374 |
1.184 |
1.350 |
1.278 |
1.203 |
1.140 |
1.048 |
0.955 |
0.864 |
0.767 |
0.675 |
0.671 |
0.660 |
0.604 |
0.574 |
0.559 |
0.496 |
0.452 |
0.405 |
0.382 |
0.330 |
0.316 |
0.299 |
0.296 |
0.276 |
0.253 |
0.237 |
0.213 |
0.196 |
4.25 |
4.5 |
4.75 |
5 |
5.25 |
2.454 |
1.963 |
1.549 |
1.193 |
0.854 |
2.418 |
1.939 |
1.510 |
1.192 |
0.839 |
2.387 |
1.938 |
1.509 |
1.163 |
0.826 |
2.319 |
1.883 |
1.474 |
1.124 |
0.800 |
2.036 |
1.664 |
1.300 |
0.980 |
0.707 |
1.540 |
1.282 |
1.030 |
0.811 |
0.640 |
1.014 |
0.869 |
0.720 |
0.597 |
0.488 |
0.595 |
0.524 |
0.446 |
0.378 |
0.329 |
0.329 |
0.296 |
0.261 |
0.224 |
0.198 |
0.179 |
0.163 |
0.142 |
0.125 |
0.112 |
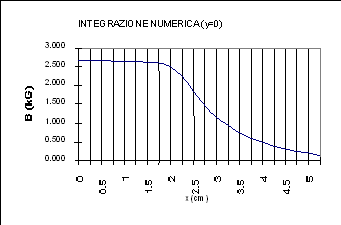
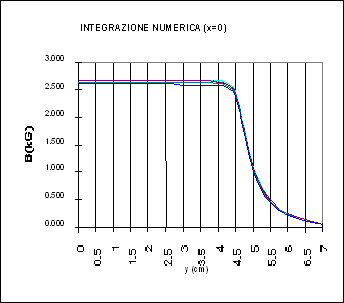
Dal valore di D V siamo in grado di risalire al valore di B in ogni punto della mappatura. L’andamento del campo magnetico all’interno e all’esterno dell’elettromagnete è chiarificato dei seguenti grafici:
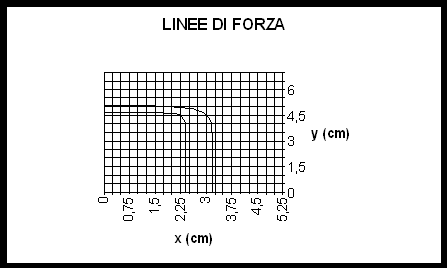

Per ricavare i valori di lunghezza e sezione fisica dell’elettromagnete abbiamo sfruttato il metodo di integrazione numerica dei trapezi, infatti noto il passo di mappatura e il corrispondente valore di B è facile approssimare l’area sottesa dalle curve B(x) e B(y) qui illustrate:
I valori numerici della lunghezza e sezione fisica sono:
Lfx = 6.21 ± 0.02 cm ; Lfy = 10.18 ± 0.04 cm ; Sf = 63.2 ± 0.3 cm2
Ora si può calcolare la riluttanza magnetica dell’elettromagnete:
![]()
per poter ricalcolare k’ tenendo conto del flusso reale nel traferro. I valori numerici sono:
R = (1.493 ± 0.007) x 106 A2/N m ; k’ = N/Sf R = 0.67 ± 0.3 kG/A