 Fig.2.1. schema delle lenti
convergenti e convenzione sul segno delle distanze coniugate p1 e p2
Fig.2.1. schema delle lenti
convergenti e convenzione sul segno delle distanze coniugate p1 e p22. FOCOMETRIA DELLE LENTI
SCOPO DELL’ESPERIENZA.
Determinazione della distanza focale di lenti sottili convergenti e divergenti mediante differenti metodi di misura.
CENNI TEORICI.
a) Lenti convergenti.
La maggior parte dei metodi per la misura della distanza focale f di una lente convergente si basa sull’equazione dei punti coniugati:
1/p1 + 1/p2 =(n - n0) (1/r1 - 1/r2) = 1/f
essendo p1 e p2 rispettivamente le distanze dell’oggetto e dell’immagine dal centro O della lente, n ed n0 l’indice di rifrazione del materiale con cui è costruita la lente e del mezzo in cui la lente è immersa ed r1 ed r2 i raggi di curvatura delle due superfici sferiche che delimitano la lente.
 Fig.2.1. schema delle lenti
convergenti e convenzione sul segno delle distanze coniugate p1 e p2
Fig.2.1. schema delle lenti
convergenti e convenzione sul segno delle distanze coniugate p1 e p2
Se l’oggetto o la sorgente si trova
all’infinito (![]() ) si ha un fascio di
luce parallela che quando incide sulla lente viene focalizzato in un piano normale
all’asse ottico( detto piano focale ). Analogamente se il fascio di luce emergente
dalla lente è costituito da raggi paralleli (
) si ha un fascio di
luce parallela che quando incide sulla lente viene focalizzato in un piano normale
all’asse ottico( detto piano focale ). Analogamente se il fascio di luce emergente
dalla lente è costituito da raggi paralleli (![]() ) la sorgente è collocata in un piano normale all’asse ottico (detto
anch’esso piano focale). La distanza tra il piano focale e il centro della lente
sottile viene indicata con il nome di distanza focale. Dall’equazione dei punti
coniugati ponendo rispettivamente
) la sorgente è collocata in un piano normale all’asse ottico (detto
anch’esso piano focale). La distanza tra il piano focale e il centro della lente
sottile viene indicata con il nome di distanza focale. Dall’equazione dei punti
coniugati ponendo rispettivamente ![]() ( fascio
incidente parallelo ) e
( fascio
incidente parallelo ) e ![]() (fascio emergente
parallelo ) si ottiene:
(fascio emergente
parallelo ) si ottiene:
1/p2 = 1/f e 1/p1 = 1/f
b) Lenti divergenti.
Il metodo ora descritto non è applicabile direttamente alla misura della distanza focale di una lente divergente in quanto essa fornisce dell’oggetto un’immagine virtuale ( formata cioè dai prolungamenti dei raggi luminosi). Si ricorre allora ad una proprietà dei sistemi di lenti per la quale se si accoppiano in maniera opportuna una lente divergente con una lente convergente il sistema ottico che ne risulta si comporta come una lente convergente. Supponendo di avere due lenti con distanze focali f1 ed f2 poste a distanza D sullo stesso asse ottico è relativamente facile dimostrare che il sistema si comporta come una lente unica di distanza focale:
F = f1 f2 /( f1 + f2 - D )
In particolare se le due lenti sono poste a contatto ( D= 0 ) si ha la relazione:
F = f1 f2 /( f1 + f2 )
che può essere riscritta nella forma:
1/F = 1/f1 + 1/f2
cioè il potere diottrico di un sistema di lenti sottili poste a contatto è semplicemente la somma algebrica dei poteri diottrici delle singole lenti. Per ottenere F > 0 nel caso di accoppiamento di una lente convergente ( f1 ) ed una lente divergente (-f2) è sufficiente che sia ½ f1½ < ½ f2½ . Con questo artificio la misura della distanza focale di una lente divergente è ricondotta alla misura di un sistema convergente essendo nota o misurata la distanza focale della lente convergente f1 .
ANALISI DEI DATI.
a) Metodo delle distanze coniugate.
Si determina il valore della distanza focale f mediante una misura delle distanze coniugate p1 e p2. Si pone una fenditura sottile ( 1 mm ) di fronte alla sorgente di luce ed a una certa distanza p1 dalla lente, si sposta quindi lungo il banco ottico lo schermo sino ad ottenere l’immagine nitida della fenditura. Misurata la distanza p2 dall’equazione dei punti coniugati si ottiene:
f = p1 p2 /( p1 +p2)
per ottenere una maggiore precisione abbiamo effettuato la misura per entrambi i fuochi rivolgendo ai raggi incidenti prima una faccia della lente e poi l’altra e facendo poi la media dei valori ottenuti.
LENTE 1 |
LENTE 4 |
||||||||
p1 |
p2 |
f |
s (f) |
p1 |
p2 |
f |
s (f) |
||
cm |
cm |
cm |
cm |
cm |
cm |
cm |
cm |
||
28.6 |
57.5 |
19.100 |
0.004 |
14.3 |
32.7 |
9.949 |
0.008 |
||
28.6 |
57.5 |
19.100 |
0.004 |
14.5 |
32.6 |
10.036 |
0.008 |
||
<f> |
s (<f>) |
<f> |
s (<f>) |
||||||
cm |
cm |
cm |
cm |
||||||
19.100 |
0.004 |
9.993 |
0.008 |
||||||
LENTE 2 |
LENTE 5 |
||||||||
p1 |
p2 |
f |
s (f) |
p1 |
p2 |
f |
s (f) |
||
cm |
cm |
cm |
cm |
cm |
cm |
cm |
cm |
||
13.7 |
39.7 |
10.185 |
0.008 |
46.5 |
84.9 |
30.045 |
0.003 |
||
13.6 |
39.8 |
10.136 |
0.008 |
46.5 |
84.8 |
30.032 |
0.003 |
||
<f> |
s (<f>) |
<f> |
s (<f>) |
||||||
cm |
cm |
cm |
cm |
||||||
10.161 |
0.008 |
30.038 |
0.003 |
||||||
LENTE 3 |
LENTE DIVERGENTE |
||||||||
p1 |
p2 |
f |
s (f) |
p1 |
p2 |
f |
f |
s (f) |
|
cm |
cm |
cm |
cm |
cm |
cm |
cm |
cm |
cm |
|
7.0 |
19.4 |
5.144 |
0.016 |
32.5 |
49.0 |
19.540 |
-21.168 |
0.004 |
|
6.7 |
19.7 |
5.000 |
0.017 |
32.5 |
49.1 |
19.556 |
-21.150 |
0.004 |
|
<f> |
s (<f>) |
<f> |
s (<f>) |
||||||
cm |
cm |
cm |
cm |
||||||
5.072 |
0.016 |
-21.159 |
0.004 |
||||||
b) Metodo dell’ingrandimento.
Fissata una distanza p1 tra la fenditura e la lente si sposta lo schermo sino ad ottenere un’immagine nitida della fenditura. L’immagine di un oggetto esteso risulta ingrandito di un fattore G rispetto all’oggetto stesso. In base alla definizione del fattore d’ingrandimento (G = A’B’/ AB ) con semplici considerazioni geometriche si ricava:
G = A’B’ /AB = P2 /P1 = f / (p1 - f)
Misurato l’ingrandimento come rapporto tra l’altezza della fenditura immagine e l’altezza della fenditura oggetto si ottiene:
f = P1 G / ( G + 1 )
| LENTE 1 | LENTE 4 |
|||||||||
| p1 | h | G | f |
s (f) |
p1 |
h |
G |
f |
s (f) |
|
| cm | mm | cm |
cm |
cm |
mm |
cm |
cm |
|||
28.6 |
25.00 |
1.976 |
18.991 |
0.015 |
14.3 |
28.00 |
2.213 |
9.850 |
0.007 |
|
28.6 |
25.00 |
1.976 |
18.991 |
0.015 |
14.5 |
28.00 |
2.213 |
9.988 |
0.008 |
|
<f> |
s (<f>) |
<f> |
s (<f>) |
|||||||
cm |
cm |
cm |
cm |
|||||||
18.991 |
0.010 |
9.919 |
0.005 |
|||||||
| LENTE 2 | LENTE 5 |
|||||||||
| p1 | h | G | f |
s (f) |
p1 |
h |
G |
f |
s (f) |
|
| cm | mm | cm |
cm |
cm |
mm |
cm |
cm |
|||
13.7 |
37.00 |
2.925 |
10.209 |
0.008 |
46.5 |
22.00 |
1.739 |
29.524 |
0.029 |
|
13.6 |
36.00 |
2.846 |
10.064 |
0.008 |
46.5 |
22.00 |
1.739 |
29.524 |
0.029 |
|
<f> |
s (<f>) |
<f> |
s (<f>) |
|||||||
cm |
cm |
cm |
cm |
|||||||
10.137 |
0.006 |
29.524 |
0.021 |
|||||||
| LENTE 3 | ||||||||||
| p1 | h | G | f |
s (f) |
||||||
| cm | mm | cm |
cm |
|||||||
7.0 |
42.00 |
3.320 |
5.380 |
0.007 |
||||||
6.7 |
41.00 |
3.241 |
5.120 |
0.007 |
||||||
<f> |
s (<f>) |
|||||||||
cm |
cm |
|||||||||
5.250 |
0.005 |
|||||||||
| LENTE DIVERGENTE | ||||||||||
p1 |
h |
G |
F |
f |
s (f) |
|||||
cm |
mm |
cm |
cm |
cm |
||||||
32.5 |
20.00 |
1.581 |
19.908 |
-20.652 |
0.016 |
|||||
28.6 |
25.00 |
1.976 |
18.991 |
-21.741 |
0.015 |
|||||
<f> |
s (<f>) |
|||||||||
cm |
cm |
|||||||||
-21.197 |
0.011 |
|||||||||
c) Metodo di Bessel.
I metodi sino ad ora descritti forniscono il valore di f quando lo spessore della lente è decisamente trascurabile rispetto alla distanza focale, il metodo di Bessel invece elimina ogni incertezza nella misura della distanza focale quando lo spessore della lente è piccolo ma non trascurabile. Con questo metodo si dispone la fenditura e la lente ad una distanza
e> 4f .
Si ricercano quindi le due posizioni in cui la lente fornisce un’immagine nitida sullo schermo. La distanza focale è data da :
![]()
dove d è la distanza tra le due posizioni, come si vede dalla figura 2.2.
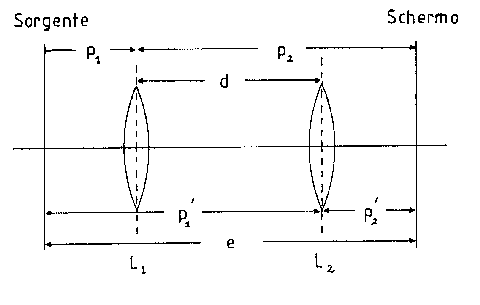 Fig.2.2. Schema illustrativo
del metodo di Bessel
Fig.2.2. Schema illustrativo
del metodo di Bessel
Abbiamo ottenuto dai dati sperimentali i seguenti risultati:
LENTE 1 |
|||||||
p1 |
p2 |
p'1 |
p'2 |
e |
d |
f |
s (f) |
cm |
cm |
cm |
cm |
cm |
cm |
cm |
cm |
23.9 |
96.1 |
96.0 |
24.0 |
120.0 |
72.1 |
19.17 |
0.04 |
23.8 |
96.2 |
95.9 |
24.1 |
120.0 |
72.1 |
19.17 |
0.04 |
<f> |
s (<f>) |
||||||
cm |
cm |
||||||
19.17 |
0.03 |
||||||
LENTE 2 |
|||||||
p1 |
p2 |
p'1 |
p'2 |
e |
d |
f |
s (f) |
cm |
cm |
cm |
cm |
cm |
cm |
cm |
cm |
12.7 |
52.4 |
52.4 |
12.7 |
65.1 |
39.7 |
10.22 |
0.04 |
12.7 |
52.4 |
52.7 |
12.4 |
65.1 |
40.0 |
10.13 |
0.04 |
<f> |
s (<f>) |
||||||
cm |
cm |
||||||
10.18 |
0.03 |
||||||
LENTE 3 |
|||||||
p1 |
p2 |
p'1 |
p'2 |
e |
d |
f |
s (f) |
cm |
cm |
cm |
cm |
cm |
cm |
cm |
cm |
6.0 |
29.1 |
28.7 |
6.4 |
35.1 |
22.7 |
5.10 |
0.04 |
6.1 |
29.0 |
28.4 |
6.7 |
35.1 |
22.3 |
5.23 |
0.04 |
<f> |
s (<f>) |
||||||
cm |
cm |
||||||
5.17 |
0.04 |
||||||
LENTE 4 |
|||||||
p1 |
p2 |
p'1 |
p'2 |
e |
d |
f |
s (f) |
cm |
cm |
cm |
cm |
cm |
cm |
cm |
cm |
12.2 |
52.9 |
52.6 |
12.5 |
65.1 |
40.4 |
10.01 |
0.04 |
12.5 |
52.6 |
52.6 |
12.5 |
65.1 |
40.1 |
10.10 |
0.04 |
<f> |
s (<f>) |
||||||
cm |
cm |
||||||
10.05 |
0.03 |
||||||
LENTE 5 |
|||||||
p1 |
p2 |
p'1 |
p'2 |
e |
d |
f |
s (f) |
cm |
cm |
cm |
cm |
cm |
cm |
cm |
cm |
38.6 |
136.1 |
135.9 |
38.8 |
174.7 |
97.3 |
30.13 |
0.04 |
38.7 |
136.0 |
136.1 |
38.6 |
174.7 |
97.4 |
30.10 |
0.04 |
<f> |
s (<f>) |
||||||
cm |
cm |
||||||
30.11 |
0.03 |
||||||
LENTE DIVERGENTE |
|||||||
p1 |
p2 |
p'1 |
p'2 |
e |
d |
F |
f |
cm |
cm |
cm |
cm |
cm |
cm |
cm |
cm |
24.9 |
100.0 |
101.4 |
23.5 |
124.9 |
76.5 |
19.51 |
-21.27 |
23.0 |
101.9 |
102.5 |
22.4 |
124.9 |
79.5 |
18.57 |
-22.51 |
<f> |
s (<f>) |
||||||
cm |
cm |
||||||
-21.89 |
0.04 |
||||||