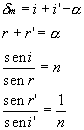
11. SPETTROMETRO A PRISMA
Scopo
Il nostro obiettivo è la misurazione dell’indice di rifrazione del vetro flint relativo all’aria in funzione della lunghezza d’onda della luce, e la verifica sperimentale della legge di dispersione secondo la formula di Cauchy.
Per la misura dell’indice di rifrazione (misura dell’angolo a del diedro di un prisma e misura dell’angolo di deviazione minima d m) e per la misura della lunghezza d’onda della radiazione incidente (mediante il prisma) si utilizza uno speciale goniometro, lo spettrometro.
Cenni di teoria
Il nostro scopo è misurare l’angolo di deviazione minima del raggio rifratto rispetto a quello incidente in funzione della lunghezza d’onda.
Indichiamo con i l’angolo di incidenza, con i’ l’angolo di emergenza e con d m l’angolo di deviazione del raggio.
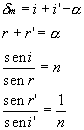
essendo a l’angolo del prisma e r ed r’ rispettivamente l’angolo di rifrazione sulla faccia di entrata del prisma e l’angolo di incidenza sulla seconda faccia del prisma.
Da queste si può ricavare la condizione di deviazione minima poiché si nota che l’angolo di deviazione d m dipende dall’angolo di incidenza i. In condizioni di minimo d m(i) deve avere derivata nulla rispetto ad i

da cui si ricava
![]()
esprimendo i coseni in funzione dei seni ed eliminando i radicali che ne derivano otteniamo:
![]()
la deviazione minima si ha quindi per
![]()
da cui ritornando al nostro sistema di equazioni di partenza ed avendo osservato che il raggio di luce si muove parallelamente alla base del prisma (se la sezione del prisma è rappresentata da un triangolo isoscele) si ricavano le espressioni per rm, d m, im

l’indice di rifrazione nel caso di minima deviazione risulta dato dalla formula:

l’indice di rifrazione dipende dalla lunghezza d’onda della radiazione incidente e il suo andamento può essere descritto con buona approssimazione dalla legge di Cauchy del tipo:
![]()
dove A e B sono due costanti caratteristiche della sostanza in esame da determinare per verificare la formula di Cauchy.
Descrizione dell’esperienza e apparato sperimentale
La determinazione di n richiede la misura dell’angolo a del prisma attraverso una lampada al sodio e successivamente una serie di misure degli angoli di minima deviazione per le varie lunghezze d’onda della luce prodotta da una lampada al mercurio.
Si utilizza una lampada al mercurio (tubo di Plucker) perché questo elemento chimico presenta delle righe intense, ben separate ed equamente ripartite su tutto lo spettro visibile.

Fig.11.1: Schema dello spettrometro recante un prisma sulla piattaforma mobile P2
Lo spettrometro è costituito da una base fissa B (vedi fig. 11.1) sul cui bordo superiore è incisa una scala goniometrica G.
Un collimatore F è solidale con la base mentre il cannocchiale C è solidale con la piattaforma girevole P1. Una seconda piattaforma girevole P2 costituisce la base di appoggio del prisma. Entrambe le piattaforme ruotano attorno allo stesso asse (normale alla base) passante per i centri delle due piattaforme. Sulle due piattaforme sono incisi quattro nonii (due a due contrapposti) che consentono la determinazione della posizione angolare sia del cannocchiale che della piattaforma P2 con un’approssimazione intorno alla trentina di secondi di grado. La lettura dei nonii è facilitata dall’uso di un oculare.
Il collimatore è costituito da un tubo che porta alle estremità una fenditura verticale regolabile in ampiezza (illuminata dalla luce prescelta) e posizionabile lungo l’asse del collimatore (entro 1 o 2 cm) ed all’altra estremità una lente convergente acromatica con una distanza focale dell’ordine della lunghezza del tubo.
Il cannocchiale dotato di un obiettivo con distanza focale di 200 –300 mm circa e di un oculare con reticolo fornisce un’immagine della fenditura con ingrandimento poco discosto dall’unità.
Prima di procedere con le nostre misure abbiamo dovuto regolare sia il collimatore sia il cannocchiale di modo che si operi in luce parallela. Abbiamo regolato in pratica l’oculare, il cannocchiale a fuoco per oggetti all’infinito e la distanza tra la fenditura e la lente convergente sino ad ottenere un’immagine nitida.
Per la misura della direzione dei raggi, provenienti dal collimatore oppure riflessi o rifratti da un prisma, si fa coincidere il reticolo dell’oculare con la mediana dell’immagine della fenditura. La posizione angolare è stata determinata mediante i due nonii contrapposti facendo la media delle due letture per evitare errori di eccentricità dell’asse di rotazione della piattaforma P1 rispetto all’asse della scala goniometrica G.
Il nostro esperimento si divide praticamente in due parti, la misura dell’angolo al vertice del prisma e la misura dell’angolo di deviazione minima rispetto ad alcune lunghezze d’onda del mercurio.
Misura dell’angolo a del prisma, processo di riflessione sulle due facce
Descrizione e analisi dei dati
Per la misura dell’angolo al vertice del prisma a si sfrutta il processo di riflessione sulle facce del prisma stesso mediante una lampada al sodio, processo che non provoca alcuna dispersione delle componenti cromatiche del fascio.
Si regola il collimatore in maniera da avere un fascio di luce parallela, si fissa il prisma sulla piattaforma e si ruota il cannocchiale sino a che esso formi con il collimatore un angolo acuto. Si fissa il cannocchiale in questa posizione e si ruota la piattaforma M che sostiene il prisma sino a vedere nel campo dell’oculare l’immagine della fenditura riflessa dalla faccia del prisma. Si fissa la piattaforma e si collima la fenditura con il reticolo agendo sulla vite micrometrica quando siamo vicini alla posizione ricercata. Si legge l’angolo q 1 sui due nonii contrapposti. Si ruota ora la piattaforma sino a sostituire la seconda faccia del prisma con la prima e si eseguono le stesse operazioni.
Da queste operazioni si può ricavare il valore di a misurando il D q = p - a = q 2 – q 1.
| 1 faccia | ||||||||
| 1 nogno | 2nogno | |||||||
q1 |
q'1 |
|||||||
° |
' |
'' |
gradi |
° |
' |
'' |
gradi |
|
26 |
0 |
0 |
26,000 |
26 |
0 |
0 |
26,000 |
|
26 |
0 |
30 |
26,008 |
26 |
7 |
30 |
26,125 |
|
26 |
7 |
0 |
26,117 |
26 |
7 |
30 |
26,125 |
|
| 2 faccia | ||||||||
| 1 nogno | 2 nogno | |||||||
q2 |
q'2 |
|||||||
° |
' |
'' |
gradi |
° |
' |
'' |
gradi |
|
86 |
9 |
30 |
86,158 |
86 |
10 |
30 |
86,175 |
|
86 |
9 |
30 |
86,158 |
86 |
10 |
30 |
86,175 |
|
86 |
12 |
0 |
86,200 |
86 |
11 |
30 |
86,192 |
|
Dai dati sperimentali si ricava questo valore di a
<a> |
s(<a>) |
|||||||
gradi |
° |
' |
'' |
rad |
gradi |
° |
' |
'' |
60,114 |
60 |
6 |
50 |
1,04919 |
0,027 |
0 |
1 |
38 |
Come ci si poteva immaginare il risultato è molto vicino ai 60° ed il grado di approssimazione di questo esperimento è elevato visto che ci risulta un valore dell’angolo al vertice di 60°7’± 0°1’38"
Misura dell’angolo di deviazione minima
Descrizione e analisi dei dati
Per misurare la deviazione minima d m abbiamo usato la lampada ai vapori di mercurio, della quale ci è noto lo spettro delle righe principali e abbiamo scelto, dopo accurata analisi le seguenti righe: le più luminose e le più facili da individuare e disposte su buona parte dello spettro della banda del visibile.
l |
|
Angstrom |
|
7081,9 |
rosso |
6907,52 |
rosso |
5803,78 |
giallo |
5460,74 |
verde |
4916,07 |
azzurro |
4358,33 |
azzurro |
4077,83 |
violetto |
4046,56 |
violetto |
Ovviamente la condizione di minima deviazione si può ottenere per una sola riga dello spettro, ma per le altre la condizione può essere ugualmente ben approssimata.
La condizione di luce parallela è importante per questo motivo, infatti nell’attraversare il prisma le differenti componenti monocromatiche presenti nello spettro della luce subiscono deviazioni diverse, tuttavia in emergenza dal prisma i raggi luminosi appartenenti alla stessa componente monocromatica si mantengono paralleli tra loro. Entrando nel cannocchiale i diversi fasci monocromatici danno luogo ad immagini reali che si formano in un unico piano in prossimità dell’oculare. Di conseguenza l’osservatore può mettere a fuoco contemporaneamente tutte le immagini prodotte dall’obiettivo.
L’impiego di luce parallela ha l’ulteriore vantaggio che tutti i raggi di determinata lunghezza d’onda attraversino il prisma in condizione di deviazione minima, ottenendo così la massima nettezza dell’immagine (anche se questa condizione può essere verificata solo per una certa riga spettrale) mentre per le altre lo è solo in maniera approssimata.
Per misurare l’angolo di deviazione minima abbiamo cercato di far entrare nel campo dell’oculare del cannocchiale l’immagine della fenditura (corrispondente ad una delle determinate righe dello spettro) rifratta dal prisma.
Le immagini della fenditura presentano una piccola distorsione (sono leggermente incurvate con concavità verso il violetto). Questo difetto è dovuto al fatto che la fenditura non è limitata in altezza. I raggi provenienti da punti della fenditura che si trovano fuori dal piano mediano arrivano al prisma inclinati verso l’alto o verso il basso. Questi raggi sono deviati maggiormente dei raggi emessi dai punti prossimi al piano mediano, dando luogo a righe incurvate verso le lunghezze d’onda più corte (violetto). Nella collimazioni siamo dovuti stare attenti anche a questo fatto per non incorrere in errori di misura.
Fatto questo abbiamo ruotato la piattaforma con il prisma sempre nello stesso verso e l’abbiamo inseguita con il cannocchiale. Abbiamo cercato di svolgere questo lavoro in due persone dandoci il cambio, poiché era difficile per una sola persona muovere entrambi gli elementi del sistema. Nella posizione in cui l’immagine inverte il senso del moto (corrispondente alla situazione di minima deviazione del prisma) bloccavamo la piattaforma e facevamo una ricerca fine con la vite micrometrica. Abbiamo dovuto stare molto attenti per la ricerca di questa condizione, perché non era di facile individuazione e non sempre si riusciva a determinare esattamente la condizione di minimo, costringendoci a ripetere varie volte la misurazione. Infine bloccavamo il cannocchiale e leggevamo sui nonii la posizione di d 1(l ) corrispondente alla lunghezza d’onda in esame (il valore è ottenuto mediante la media dei due nonii contrapposti, sempre per evitare errori di ellissi).
Abbiamo ripetuto questa procedure per tutte le righe prese in esame:
| 1 nogno | 2 nogno | ||||||||||
d1 |
d'1 |
l |
|||||||||
° |
' |
'' |
gradi |
° |
' |
'' |
gradi |
Angstrom | |||
156 |
30 |
30 |
156,508 |
156 |
29 |
30 |
156,492 |
7081,9 |
rosso |
||
156 |
7 |
30 |
156,125 |
156 |
5 |
0 |
156,083 |
6907,52 |
rosso |
||
155 |
48 |
0 |
155,800 |
155 |
48 |
0 |
155,800 |
5803,78 |
giallo |
||
155 |
53 |
0 |
155,883 |
155 |
50 |
0 |
155,833 |
5460,74 |
verde |
||
154 |
43 |
30 |
154,725 |
154 |
45 |
0 |
154,750 |
4916,07 |
azzurro |
||
153 |
46 |
30 |
153,775 |
153 |
46 |
30 |
153,775 |
4358,33 |
azzurro |
||
153 |
6 |
0 |
153,100 |
153 |
8 |
0 |
153,133 |
4077,83 |
violetto |
||
152 |
46 |
0 |
152,767 |
152 |
45 |
0 |
152,750 |
4046,56 |
violetto |
||
Terminate queste misure sulle diverse lunghezze d’onda abbiamo tolto il prisma e abbiamo ruotato il cannocchiale sino a collimare l’immagine diretta della fenditura, così da poter registrare l’angolo di posizione angolare di collimazione dell'immagine della fenditura, senza il prisma per i due nonii contrapposti:
d0 |
d'0 |
|||||||
° |
' |
'' |
gradi |
° |
' |
'' |
gradi |
|
24 |
27 |
0 |
24,45 |
24 |
27 |
0 |
24,45 |
Ed abbiamo ottenuto il dato sperimentale dell’angolo di deviazione minima per le varie lunghezze d’onda applicando:
![]()
l |
dm |
||||
Angstrom |
gradi |
° |
' |
'' |
rad |
7081,9 |
47,950 |
47 |
56 |
60 |
0,8369 |
6907,52 |
48,346 |
48 |
20 |
45 |
0,8438 |
5803,78 |
48,650 |
48 |
38 |
60 |
0,8491 |
5460,74 |
48,592 |
48 |
35 |
30 |
0,8481 |
4916,07 |
49,713 |
49 |
42 |
45 |
0,8676 |
4358,33 |
50,675 |
50 |
40 |
30 |
0,8844 |
4077,83 |
51,333 |
51 |
19 |
60 |
0,8959 |
4046,56 |
51,692 |
51 |
41 |
30 |
0,9022 |
Mediante la
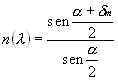
si ottengono i valori per n(l ) sperimentali:
n(l) |
s(n) |
1,616 |
0,005 |
1,620 |
|
1,623 |
|
1,622 |
|
1,634 |
|
1,643 |
|
1,650 |
|
1,653 |
Dai quali con il metodo dei minimi quadrati si determinano i valori di A e B per la formula di Cauchy:
![]()
usando
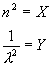
si ottiene il grafico della miglior retta

con
c 2 /n |
n |
probabilità |
0,91243361 |
6 |
48,45% |
Ed i valori di A e B per la formula di Cauchy dati da:
| B | s(B) |
A | s(A) |
2,82E+06 |
2,4,E+05 |
2,55326 |
2,1E-05 |
Dai quali ricaviamo il valore dell’indice di rifrazione del prisma al variare delle diverse lunghezze d’onda con un grado di approssimazione pari a ± 0,005:
| INDICE DI RIFRAZIONE (l ) | ||
nfit(l ) |
l |
|
| Angstrom | ||
1,615 |
7081,9 |
rosso |
1,616 |
6907,52 |
rosso |
1,624 |
5803,78 |
giallo |
1,627 |
5460,74 |
verde |
1,634 |
4916,07 |
azzurro |
1,644 |
4358,33 |
azzurro |
1,650 |
4077,83 |
violetto |
1,651 |
4046,56 |
violetto |
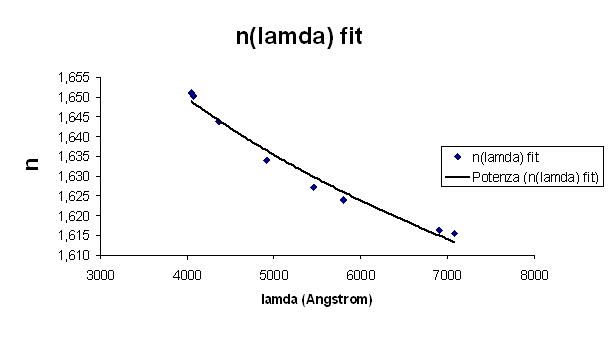 Questi dati corrispondono a quelli di vetro flint pesante con
un buon grado di approssimazione, infatti nel rosso a 768nm ha un valore di n = 1.638,
mentre nel violetto a 361nm ha un valore di n = 1.705
Questi dati corrispondono a quelli di vetro flint pesante con
un buon grado di approssimazione, infatti nel rosso a 768nm ha un valore di n = 1.638,
mentre nel violetto a 361nm ha un valore di n = 1.705
INDICE DI RIFRAZIONE PER IL FLINT PESANTE |
|
nflint pesante(l) |
l |
Angstrom |
|
1,638 |
7680 |
1,644 |
6560 |
1,65 |
5890 |
1,664 |
4860 |
1,675 |
4340 |
1,705 |
3610 |
Questo metodo ha dato dei buoni risultati, e ci ha permesso di verificare la legge di dispersione secondo la formula di Cauchy con un ottimo grado di probabilità.